平均单元厚度
第 11 个用户材料常数定义与基于能量的降级结合使用的平均单元厚度。对于二维单元，则忽略此值。对于三维（实体）单元，这是与材料相关联的实体单元的平均厚度，其中该厚度被定义为单元的层间尺寸。
从附录 A.5 重新调用，该附录可提供基于能量的降级计算中所使用的最终有效应变。
在上述部分中，如 Abaqus 定义的那样，Le 是代表单元长度。对于三维单元（即块体和连续壳），单元长度为体积的立方根。对于二维单元（即壳和平面应力单元），单元长度为面积的平方根。
对于二维单元，将忽略单元厚度。代表单元长度提供了对单元的平面内区域进行测量的方法，这为我们提供有意义的测量值，以便与合成层相关联。但是，对于分层实体单元，代表单元长度与单个层的测量值没有任何关联。若要适应实体单元的使用并允许针对二维实体的结果对它们加以使用和比较，必须修改代表单元长度，以在层的平面内提供有用的单元长度测量方法。
复合断裂几乎总是在层的平面中发生。因此，忽略单元的厚度方向大小更加精确。此操作通过使用用户材料定义中提供的平均单元厚度常数完成。然后，代表单元长度的计算方法如下所示：
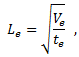
其中 Ve 是单元的体积，te 是单元的平均厚度。以上方程中定义的单元长度提供了对实体单元的平面内区域进行精确测量的方法，并且当实体单元的厚度是一个常数时，将折叠到 Abaqus 为二维单元提供的精确测量值。
降级时间段
在使用瞬时降级的 Abaqus/Explicit 分析中，立即降级材料特性可能会对结构的响应产生负面影响。刚度变化率较大的局部材料响应可能会在材料中生成冲击波，从而在相邻单元中过早地萌生损坏。为了减轻这种影响，我们指定了一个时间段，以便在该时间内通过用户材料常数 11 降级材料特性。此值必须大于或等于 0。时间段越长，刚度变化率将越小。
如果失效萌生，材料特性不是自动缩减到下一个材料状态。材料刚度依据以下方程更新：
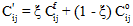
其中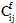 
和 
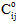分别是下一个材料状态和上一个材料状态下的材料刚度，
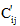是更新后的（中间）材料刚度。
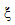被定义为：
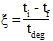
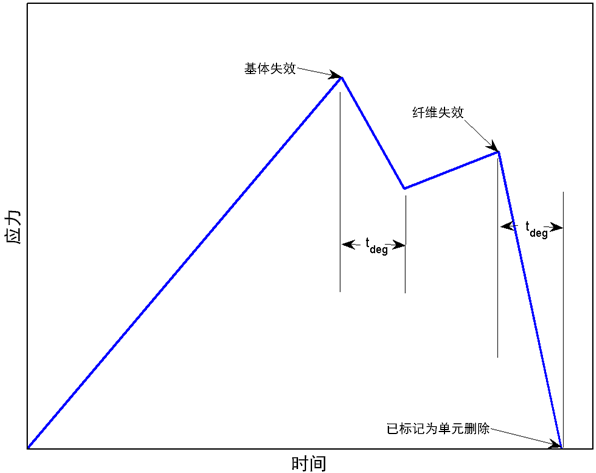
其中 ti、tf 和 tdeg 分别是当前时间、失效萌生时间和降级时间段（用户材料常数 11）。下图针对时间降级期限的不同值（失效萌生后的常数应变）以时间函数的形式对局部材料响应进行了描述。
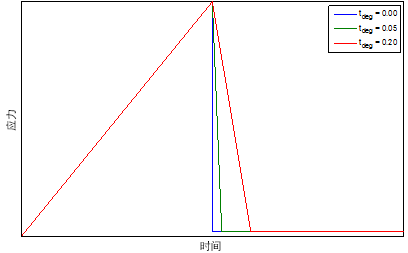
有关积分点处与时间相关的应力的理想化示例，请看下图。
