本部分介绍单向和织物复合材料的成分平均应力及应变状态概念。
发展了这些量的简单派生,并讨论了使用成分平均量的优点和限制。
σ(x,y,z) 表示实际应力张量场,该值随异构微观结构的每个成分材料中位置的改变而改变。D 表示足以在某个点特征化复合材料响应的代表性体积单元 (RVE) 的域。无论 RVE 内实际应力分布的复杂性如何,RVE 内的复合平均(或均质)应力状态 σC 均可表示为

其中 V 是 RVE 的总体积。同样,纤维和基体平均应力状态可以表示为

其中,Vf 和 Vm 分别是 RVE 内纤维和基体成分的体积 (V=Vf +Vm),而 Df 和 Dm 分别表示由 RVE 内纤维和基体成分占用的子域 (D = Df 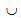 Dm)。合并 Eq. 1-3 将生成
Dm)。合并 Eq. 1-3 将生成

其中 φf = Vf/V 和 φm = Vm/V 分别是纤维和基体成分材料的体积因子。
类似的推理方式同样适用于应变张量,从而可以生成下面的 Eq. 5-8。

关于 Multicontinuum 理论的使用的基本观点是,成分平均应力和应变状态(σf、σm、εf、εm)在预测损坏演变和材料失效方面比复合平均应力和应变状态(σc、εc)更具相关性。基体成分中的损坏演变和失效实际上由基体成分材料中的应力和应变推动,不是由纤维成分材料中的应力和应变推动,也不是由均质复合材料中的应力和应变推动。对于纤维成分,道理类似。
尽管对于平均各个成分中的实际微观机械应力场来提供优质信息以便预测复合材料中的损坏演变和失效,这很容易就能理解,但应全面考虑与各种平均应力状态有关的体积平均过程的过滤特征。让我们从考虑受简单均质复合应力状态 σc 约束的单向纤维增强复合材料的代表性体积单元着手。例如单轴应力状态,其中 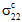 > 0,而其他所有
> 0,而其他所有 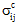 = 0。尽管复合平均应力状态是单轴的,但 RVE 的异构微观结构中的实际微观机械应力场 σ(x,y,z) 却十分复杂。这归因于由成分材料的刚度、泊松比和热膨胀系数中的差异而造成它们之间出现自平衡交互。例如,在实际微观机械应力场中,六个应力分量中有四个分量(σ11、σ22、σ33、σ23)在 RVE 内达到非零值。此外,这四个应力分量通过大量的局部化应力集中,显示了 RVE 上的高度空间变化。但是,三个实际应力分量(σ11、σ33、σ23)完全是由于成分材料之间的自平衡交互所致。例如,纤维和基体的泊松比差异会影响对自平衡 σ11(x,y,z) 和 σ33(x,y,z) 应力场的研究。如果存在空间变化的 σ11(x,y,z)、σ22(x,y,z) 和 σ33(x,y,z) 应力场,剪切应力必须出现才能维持局部平衡。方程 9-11 显示平衡的偏微分方程已简化,以适用于当前所有应力分量均相对于纤维方向(即“1”方向)保持不变的单向复合 RVE 的情形。
= 0。尽管复合平均应力状态是单轴的,但 RVE 的异构微观结构中的实际微观机械应力场 σ(x,y,z) 却十分复杂。这归因于由成分材料的刚度、泊松比和热膨胀系数中的差异而造成它们之间出现自平衡交互。例如,在实际微观机械应力场中,六个应力分量中有四个分量(σ11、σ22、σ33、σ23)在 RVE 内达到非零值。此外,这四个应力分量通过大量的局部化应力集中,显示了 RVE 上的高度空间变化。但是,三个实际应力分量(σ11、σ33、σ23)完全是由于成分材料之间的自平衡交互所致。例如,纤维和基体的泊松比差异会影响对自平衡 σ11(x,y,z) 和 σ33(x,y,z) 应力场的研究。如果存在空间变化的 σ11(x,y,z)、σ22(x,y,z) 和 σ33(x,y,z) 应力场,剪切应力必须出现才能维持局部平衡。方程 9-11 显示平衡的偏微分方程已简化,以适用于当前所有应力分量均相对于纤维方向(即“1”方向)保持不变的单向复合 RVE 的情形。

方程 10 和 11 表示剪切应力分量 σ23 必须在 RVE 内的任意点处演变,其中 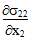 或
或 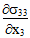 为非零值。遗憾的是,这些自平衡应力分量(σ11、σ33、σ23)已由于在整个 RVE 上平均微观机械应力场而被完全过滤,由此复合平均应力状态是单轴的并且
为非零值。遗憾的是,这些自平衡应力分量(σ11、σ33、σ23)已由于在整个 RVE 上平均微观机械应力场而被完全过滤,由此复合平均应力状态是单轴的并且 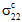 > 0。
> 0。
关于复合平均应力状态 σc 无法表示自平衡应力分量的最佳例证是,不受约束的复合材料受到均匀温度变化的作用。在此情况下,实际应力场 σ(x,y,z) 的所有四个非零分量(σ11、σ22、σ33、σ23)为自平衡,并且由于两种成分材料热膨胀系数的差异所致。复合平均应力状态恒为零 (σc= 0)。但是,对于较大的温度变化,实际微观机械应力场 σ(x,y,z) 的非零分量(σ11、σ22、σ33、σ23)可能太大,导致损坏演变或材料失效。
与在计算复合平均应力状态过程中发生的严格过滤相比,计算成分平均应力状态的过程仅过滤该特定成分材料上自平衡的应力分量。应该强调的是,由于成分泊松比或热膨胀系数的差异引起的自平衡法线应力在 RVE 上作为整体自平衡,而不是在任一成分上自平衡。因此,成分平均应力状态不会过滤出这些自平衡法线应力。另一方面,要取得进展以维持局部平衡的自平衡剪切应力是自平衡,即使是在每个成分材料内也是如此。因此,复合平均应力状态和成分平均应力状态均会过滤自平衡剪切应力。
根据前面的讨论,下表总结了成分平均应力状态的过滤特征。
- 通常,应用一个或多个复合平均法线应力(例如
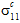 、
、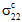 和/或
和/或 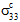 )会产生三轴的成分平均应力状态(即,所有三个法线应力均非零)。即使复合应力状态是单轴的(例如
)会产生三轴的成分平均应力状态(即,所有三个法线应力均非零)。即使复合应力状态是单轴的(例如 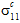 ≠ 0,并且其他所有
≠ 0,并且其他所有 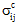 = 0),此观点仍成立。这是成分材料之间泊松交互的直接结果。当在整个 RVE 上集成时,因成分泊松比之间的差异生成的法线应力为自平衡,但在单个成分上集成时却不是自平衡的。因此,成分平均应力状态会保留由外部机械载荷生成的法线应力和由成分间泊松交互所致的法线应力。
= 0),此观点仍成立。这是成分材料之间泊松交互的直接结果。当在整个 RVE 上集成时,因成分泊松比之间的差异生成的法线应力为自平衡,但在单个成分上集成时却不是自平衡的。因此,成分平均应力状态会保留由外部机械载荷生成的法线应力和由成分间泊松交互所致的法线应力。
- 如果不受约束的复合材料受到均匀温度变化的作用,则成分的热膨胀系数的差异将导致自平衡热应力在整个 RVE 上集成时取得进展,但在单个成分上集成时不是自平衡的。在这种情况下,复合平均应力状态恒为零 (σc = 0)。但是,成分平均应力状态为三轴(即
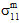 ≠ 0、
≠ 0、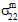 ≠ 0、
≠ 0、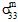 ≠ 0、
≠ 0、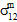 =
= 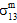 =
= 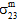 = 0 且
= 0 且 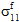 ≠ 0、
≠ 0、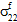 ≠ 0、
≠ 0、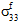 ≠ 0、
≠ 0、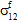 =
= 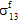 =
= 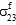 = 0)。
= 0)。
- 单向纤维增强复合材料为正交各向异性(或横向各向同性),因此不会显示法线应力和剪切应力之间的耦合。一般而言,有两种不同的方法可以在复合材料中生成剪切应力。第一,外部应用的机械载荷可以在复合材料中生成剪切应力,并且这些剪切应力不是自平衡的。因此,复合平均应力状态 (σc) 和成分平均应力状态(σf 和 σm)包含这些剪切应力的测量。第二,生成自平衡剪切应力场,来维持存在显示 RVE 内空间变化的法线应力时的局部平衡(根据偏微分方程)。实际上,这些剪切应力在 RVE 内的每个成分材料中是自平衡的。因此,复合平均应力状态 (σc) 和成分平均应力状态(σf 和 σm)都不包含这些自平衡剪切应力的任何测量。
尽管普遍认为实际微观机械应力场 σij(x,y,z) 会导致个别成分材料及其材料界面中的损坏演变和失效,但开发直接使用实际微观机械应力场的模型却是一个惊人、复杂且计算麻烦的提议。在 Multicontinuum 理论中,我们转为关注成分平均应力状态概念,在此概念中,实际微观结构应力场 σij(x,y,z) 在微观结构的每个成分材料上平均体积。但是,为了在结构级别的分析中有效利用成分平均应力状态,请务必发展计算成分平均应力状态的非常有效的方法。出于实际原因,对复合结构的结构级别分析会根据复合平均应力状态来制定。因此,使用成分平均应力状态需要将复合平均应力状态分解为成分平均应力状态的方法。这一称为 MCT 分解的过程将在下一部分中介绍。