热残余应力

考虑热残余应力对单向复合材料的影响。

**当前，仅可以针对单向复合材料计算热残余应力，而不可以针对织物复合材料计算热残余应力。

微观结构效应

在室温 T=T_amb 中，独立、未加填料、不受约束、单向复合材料层的纤维和基体成分已经具有非零应力状态。这是由复合材料从固化温度 T=T_cure 到环境温度 T=T_amb 的固化后冷却造成的。在独立的复合层中，这些热残余应力仅由基体和纤维成分的热膨胀系数的差异引起的。通常，在纤维增强的复合材料层固化后冷却期间，基体成分将尝试收缩得比纤维成分的更多。因此，基体成分将显示拉伸热残余应力，纤维成分将显示压缩热残余应力。但是，合成平均应力状态为零。这些成分热残余应力会在任何后续热机械载荷复合材料层期间对总成分应力状态造成影响，进而影响成分失效发生时的载荷。

分层效应

当复合材料层嵌入经历固化后冷却的层中时，会诱发复合材料层中的其他热残余应力。这是由涉及的层及其相邻层的热膨胀系数之间的差异造成的。不同于独立的复合材料层，此类型的层内作用会导致层级别的合成平均应力状态为非零，即该层会发起合成平均热残余应力。这些应力可以分解为纤维和基体平均热残余应力，它们在后续热机械载荷期间会对总纤维和基体平均应力状态产生影响。因此，应力会影响成分失效发生时的载荷。

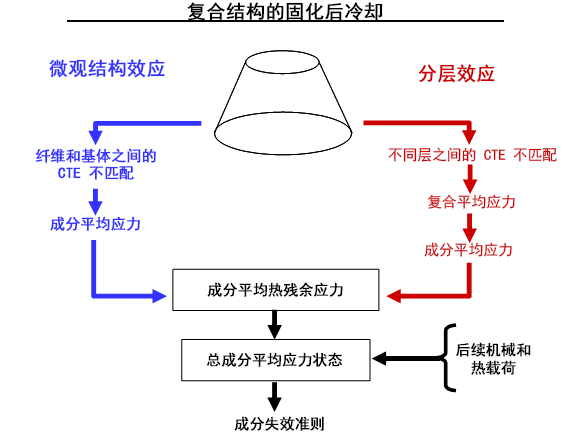
成分材料级别的这两个热残余应力源如以下示意图所示。如图所示，成分热残余应力添加到法向外部应用机械和热载荷的结构所生成的成分应力。

计算 Helius PFA 中的热残余应力

方程 32a-c 列出的线性化、热机械本构关系（割线公式）适用于单向复合材料、基体成分材料和纤维成分材料。

在方程32a 中，某一点处的总合成应变状态 (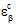) 由结构性有限代码直接提供，而在方程32b 和 32c 中，使用 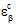的 MCT 分解确定某一点处的总成分应变状态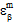（ 和 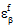）。对于温度相关复合材料，刚度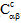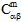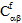（、、）和热膨胀系数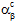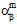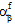（、、）取决于当前温度 T 以及纤维和基体成分材料的当前失效状态。对于温度无关复合材料，刚度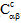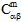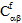（、、）和热膨胀系数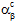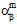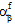（、、）仅取决于纤维和基体成分材料的当前失效状态。

在方程 32 中，一个通常预想的温度变化 ΔT 为复合材料的当前温度与复合材料的无应力温度 T_sf 之间的差值，即 ΔT = T - T_sf。然而，Helius PFA 实际使用何种表达式来计算 ΔT 取决于您是否希望考虑复合材料的固化后冷却期间积累的热残余应力。通过适当用户材料常量的整数值来为任何复合材料开关此功能（请参见《Helius PFA 用户指南》的附录 A）。

热残余应力处于“关闭”状态

如果热残余应力功能处于“关闭”状态，则在模拟过程中热残余应力将不包含在单向复合材料的响应中。在这种情况下，复合材料的无应力温度默认为 T_sf = 0°，而在方程32 中使用的温度变化将仅按以下方式进行计算：ΔT = T - T_sf = T。对于热残余应力计算处于“关闭”状态的情况，应强调以下几点。

1. 无应力温度 T_sf 的默认值为 0°，即使复合材料数据文件（mdata 文件）明确定义了一个非零无应力温度也是如此。
2. 无论有限元模型采用何种单位制，当前温度 T 都将完全定义方程32.
3. 对于在多个温度下特征化的复合材料，当前温度 T 将用于插入方程32 中出现的材料特性。因此，如果忽略复合材料的热残余应力，建议将单温度特征化（即，单温度 mdata 文件）用于涉及的复合材料。

总之，对于忽略热残余应力的情况，当前温度 T 通过两种不同方法影响方程32：

1. T 用于定义 ΔT，通过 ΔT=T。
2. T 用于插入材料特性的当前值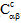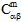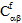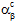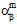：、、、、 和 。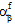

热残余应力处于“打开”状态

如果热残余应力计算功能处于“打开”状态，则在模拟过程中热残余应力将明确包含在复合材料的响应中。在这种情况下，将从 MCT 复合材料数据库文件（mdata 文件）中读取复合材料的无应力温度 T_sf，其中 T_sf 将被理解为与材料的固化温度 T_cure 同义。如果材料的无应力温度 T_sf 未在 mdata 文件中明确定义，Helius PFA 会生成错误消息，指示必须定义无应力温度。

当热残余应力计算功能处于“打开”状态时，有两种方法可用于计算方程32 中使用的温度变化，具体取决于是否为当前温度使用材料特性，或者是否指定一组唯一材料特性。

当前环境

在使用当前特性的默认情况下，温度变化的计算方法如下：

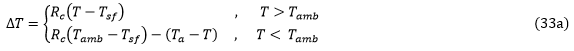
在方程33a 中，T_amb 为环境温度（可理解为 72.5 °F、22.5 °C 或 295.65 °K），具体取决于模型中所使用的单位制。T 为当前温度，T_sf 为无应力温度。

如果当前温度 T > T_amb，方程33a 确保在固化后冷却结束时正确预测热残余应力。量 R_c 表示固化比。默认情况下，R_c 的值设为 0.5。该默认值基于 Kenik [13] 的作用。Kenik 表明：一个简单线性弹性分析（使用室温复合材料特性以及实际固化后冷却施加温度减半）所产生的成分热残余应力，约等于更严格的微机械使用温度相关基体特性模拟固化后冷却所预测的成分热残余应力。要调整 R_c 的值，请参考 Abaqus 或 ANSYS 用户手册中的“热残余应力”主题。

如果当前温度 T < T_amb，方程33a 确保在固化后冷却之后施加的任何其他温度减少都将产生正确的热应力。在这种情况 (T < T_amb) 下，方程 32 中 Helius PFA 所使用的总体温度变化 ΔT包含从无应力温度 T_sf 到环境温度 T_amb 50%（使用 R_c 的默认值）的温度变化。它还包括从环境温度 T_amb 到当前温度 T 100% 的其他温度减少。但是，如果当前温度 T 等于或高于环境温度 T_amb，则方程 32 中 Helius PFA 所使用的总体温度变化 ΔT 将只考虑从无应力温度 T_sf 到当前温度 T 50%（使用 R_c 的默认值）的实际温度变化。请注意，如果材料重复加热到固化温度 T_cure，则计算 ΔT 的此方法确保热残余应力会消失。

请注意，如果 T = T_amb，方程33a 则减少到同一方程。

指定环境

对于在环境温度中将一组唯一材料特性用于计算的情况，温度变化分两个步骤计算。首先，对于从固化温度到环境温度的变化（步骤 A），其次，从环境温度到当前温度的变化（步骤 C）。（步骤 B，涉及从固化环境到周围环境的湿度变化。）

对于步骤 A，使用环境湿度和温度的材料特性。对于步骤 C，使用当前湿度和温度的材料特性。

在方程33b 中，{ } 为 Macaulay 括号，其中 {x}=0（对于 x<0）；{x}=x（对于 x ≥ 0）。T_amb 为在 HIN 文件中 *CURE STRESS 关键字内指定的环境温度。如果未指定温度，T_amb 可以理解为 72.5 °F、22.5 °C 或 295.65 °K，具体取决于模型中使用的单位制。T 为执行测试的温度（当前温度）。

方程33b 右侧确保在固化后冷却结束时，热残余应力正确预测为环境温度（即，当 T=T_amb 时）。R_c^A 量表示此步骤的固化比。默认情况下，R_c^A 的值设为 0.5。该默认值基于 Kenik [13] 的作用。Kenik 表明：一个简单线性弹性分析（使用室温复合材料特性以及实际固化后冷却施加温度减半）所产生的成分热残余应力，约等于更严格的微机械使用温度相关基体特性模拟固化后冷却所预测的成分热残余应力。要调整 R_c^A 的值，请参考 Abaqus 或 ANSYS 用户手册中的“热残余应力”主题。

方程33c 右侧确保在固化后冷却之后施加的任何其他温度减少都将产生正确的热应力。请注意，使用 Macaulay 括号 { } 确保：仅在当前温度 T 高于环境温度 T_amb 时，方程 33c 右侧的第一项才会影响 ΔT。R_c^C 量表示此步骤的固化比。默认情况下，R_c^C 的值设为 0.5。要调整 R_c^C 的值，请参考 Abaqus 或 ANSYS 用户手册中的“热残余应力”主题。如果当前温度 T 低于环境温度 T_amb，表明未应用固化比。

总温度变化 ΔT = ΔT^A + ΔT^C。

MCT 复合材料特征化

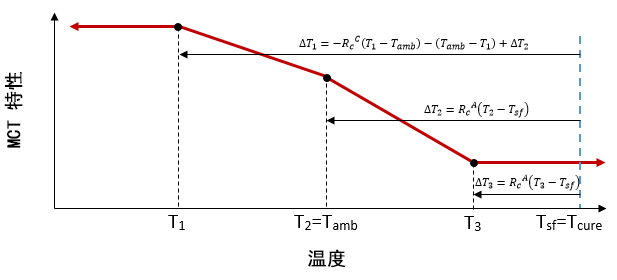
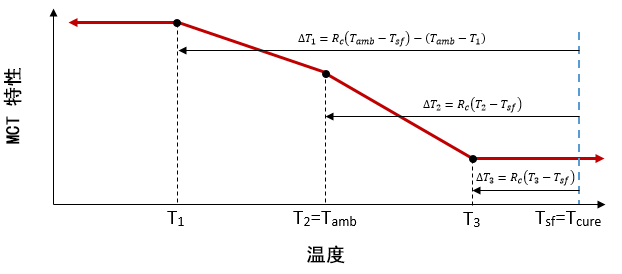
方程32 和 33 还可用于针对多种温度下特征化的材料进行 MCT 材料特征化处理。如下图所示的典型情况，温度相关复合材料在三个不同温度 T₁、T₂ 和 T₃（其中，T₁<T_amb、T₂=T_amb 和 T_amb<T₃<T_cure）下完成特征化。在 MCT 特征化过程中，它还显示温度变化 ΔT（通过方程3a-c 进行计算），该温度变化包含在这三个温度中每一个处的复合材料的微机械分析中。在特征化过程中，这些施加的温度变化会影响成分失效系数的确定。例如，当微机械模型机械地加载到已测量的失效载荷级别时，成分复合材料中的失效应力状态具有的影响来自机械载荷和施加的温度变化。

当前环境

指定环境