检查如何针对渐进式疲劳处理振荡应力。
之前页面中的讨论提供了一种方法，用于将应力张量减少到一个标量值。现在，我们来解决如何考虑振荡应力的问题。术语应力比 R 和平均应力 σm 的引入通常用于描述因应力不同（从某些最小应力 σmin 到某些最大应力 σmax）而有所不同的简单正弦载荷，其中
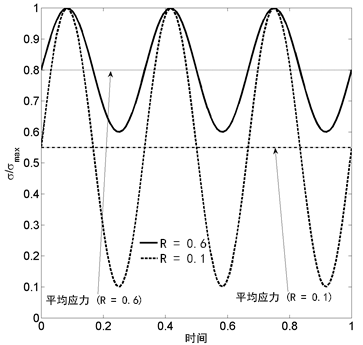
考虑上面显示的载荷历史记录：R = 0.1 和 R = 0.6。如果应力是唯一随时间变化的量，作为时间函数的粘合断裂率可以写为
并且粘合修复率可以写为
通过对 Eq. 52 和 53 进行积分，可以表明动力学理论预测通过增加 σmin 来增加平均应力会导致在 R 值增加的同时缩短疲劳寿命。从另一个角度考虑恒定载荷工况 R = 1。很明显，增加平均应力将减少失效时间。但有关单向和织物复合材料的实验表明，提高 σmin 将导致疲劳寿命的增加 [47, 25-26]。因此，应力的振荡性质似乎呈现了在恒定载荷下不存在的额外物理特征。
这个额外的物理特征就是循环过程中聚合物的温度变化。有关纯聚合物的实验结果表明，这些聚合物的温度随着振荡应力振幅 [28, 35] 的增加或随着频率 [48] 的增加而急剧升高。为了使动力学理论正确预测任何载荷记录的疲劳寿命，必须将此类温度的升高考虑在内。对于正弦周期，每秒能量耗散率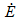 
由 [28] 得出：
其中 f 是振动频率，J'' 是损耗柔量，σa 是应力振幅。我们假定温度升高量与耗散的能量成比例。Eq. 40 中使用的温度 T 由如下标称温度 T* 计算得出
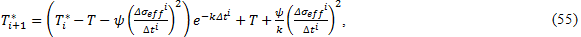
其中 ψ 是比例常数，k 是牛顿冷却定律常数，Δσeff 是有效应力随 Δt 时间跨度更改的幅度，而 n 是每个循环不同应力范围的数量 [26]。下图显示了 Δσeff 和 Δt 的值如何在单次载荷循环中确定。
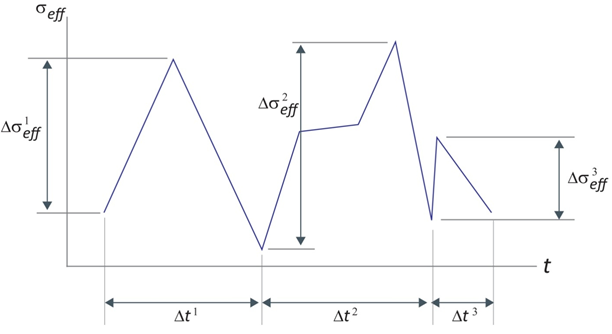
在 Eq. 55 中使用牛顿冷却定律能够使材料温度在很长一段时间内都稳定在周围环境的温度，而不是无限升高。