开发双成分(纤维/基体)复合材料的关系。
在结构级别分析中,我们可以在复合结构中的任何材料点直接访问复合平均应力和应变状态(σc 和 εc)。在本部分中,我们将为双成分(纤维/基体)复合材料开发关系,该关系允许 εc 分解为成分平均应力和应变状态(σf、εf、σm、εm)。上一部分的方程 4 和 8 将提供此 MCT 分解的框架,这些方程对任何材料响应和所有分解级别有效。
MCT 分解开发的第一步是调用适用的本构关系,该本构关系以相应的平均应变度量表示平均应力度量。我们施加本构关系为线性的限制,以便使 MCT 分解保持唯一,并且在数学上已处理。我们将在稍后看到,对线性本构关系的限制不会造成严重限制;仍然可以在非线性问题中利用 MCT 分解。方程 12-14 列出了各种可使用的体积平均线性化本构关系。
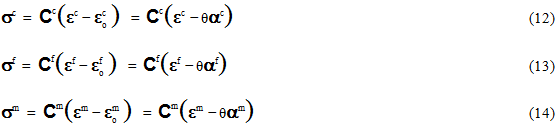
在 Eq. 12-14 中,Cc、Cf 和 Cm 分别表示均质复合材料、纤维成分和基体成分材料的 6x6 本构矩阵(正割公式)。θ 表示相对于在其中测量材料特性的均匀参照温度的复合材料均匀温度变化。项 αc、αf 和 αm 是分别表示均质复合材料、纤维成分和基体成分材料的热膨胀系数的 6x1 矢量。由于本构关系为线性,因此 Cc、Cf、Cm、αc、αf 和 αm 的各个分量仅为常数。但是,若要将 MCT 分解应用到非线性问题,假定本构关系 (Eqs. 12-14) 关于当前状态线性化(由 σC、εC、σF、εF、σM、εM 和 θ 定义)。此方法与非线性结构级别分析中常用的方法完全一致,在非线性结构级别分析中,复合结构的总体非线性响应由分段线性响应的序列表示。
接下来,将线性化本构关系 (Eqs.12-14) 代入 Eq. 4,得到
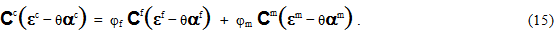
进一步将 Eq. 8 代入 Eq. 15 得到
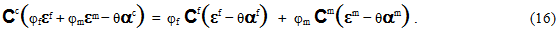
Eq. 16 现在可以针对纤维平均应变状态 (εf) 进行求解,方法是将同类项分组并将它们乘以 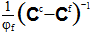 ,得到
,得到
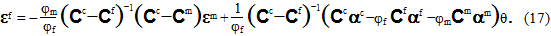
此时,您可以轻松理解之前对线性化本构关系施加的限制。具体而言,如果 Cc、Cf、Cm、αc、αf 和 αm 的分量不是常数,则得出 Eq. 17 的代数不可处理。
为方便起见,我们现在定义一个 6x6 矩阵 A 和一个 6x1 矢量 a,如下所示。
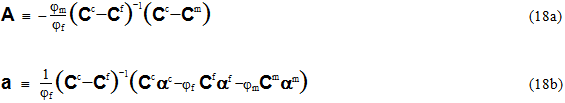
使用这些新定义的量,Eq. 17 可以简写为

请注意,矩阵 A 关联成分中的平均机械应变,而 a 关联成分中的平均热应变。方程 19 现在可用于消除平均纤维应变 εf(从 Eq. 8 中),根据复合平均应变状态 εc 得到基体平均应变状态 εm 的表达式。

计算基体平均应变状态 εm(通过 Eq. 20)后,纤维平均应变状态 εF 只需使用 Eq. 8 计算,如下所示

在计算基体和纤维平均应变状态(εm 和 εf)后,基体和纤维平均应力状态(σm 和 σf)可以使用线性化本构关系计算(Eqs. 13 和 14)。
总结起来,MCT 分解的分析形式由四个方程(Eq. 20、21、13 和 14)组成,这四个方程用于将材料点的复合平均应变状态分解为相同材料点的成分平均应变和应力状态。可在已知复合平均应变状态的复合结构内的任何点非常高效地执行此分解。MCT 分解是一项使能技术,用于更好地以物理方式观察异质复合微观结构的状态。正如我们稍后会看到的,了解成分平均应力和应变状态的主要好处是改进了预测复合微观结构的成分材料内的损坏演变和材料失效的物理基础。
MCT 分解的基础方程由 Eq. 20 提供,该方程可视为一个传递函数,用于将复合平均应变状态 εc 映射到基体平均应变状态 εm 中。对于表现出非线性响应的复合材料,重新迭代使用 Eq. 20 的含义是值得的。首先,将 εc 映射到 εm 中完全由量 Cc、Cf、Cm、αc、αf、αm、φf 和 φm 定义,这些量假定为常数。因此,对于非线性材料响应或有限变形,本构关系 (Eqs. 12-14) 必须关于当前材料状态线性化(由 σC、εC、σF、εF、σM、εM和 θ 定义)。此限制的含义是,复合材料的总体非线性响应必须由线性响应的有限序列表示,其中 Cc、Cf、 Cm、αc、αf 和 αm 可视为响应的每一个段内的常数。在实践中,响应每一段的 MCT 分解都不同,因为 Cc、Cf、Cm、αc、αf 和 αm 在段与段之间不同。同样,此材料响应的分段线性表示形式与执行非线性结构级别分析时常用的方法完全一致。
还应强调,MCT 分解(总体上为 Eqs. 20、21、13、14)需要最少的计算工作量。因此,可以将其应用到结构级别分析中的所有关注点,而无需大幅增加总体计算时间。例如,在复合结构的结构级别有限元分析中,在模型中的每个高斯积分点使用 MCT 分级通常只会增加总求解时间 2%-3%。
对于简单、单向的纤维增强复合材料,分析二进制分解尤其有优势。Helius PFA 为所有单向增强复合材料使用分析二进制分解。即使对于织物或编辫复合材料,从牵引平均应力和应变到纤维和基体平均应力和应变的最终分解仍使用分析二进制分解来执行。