织物微观结构开发

查看织物材料的几何图形、微观结构和限制的详细信息。

几何图形生成

当前，Composite Material Manager 支持五种类型的微观结构。第一个和最简单的是由嵌入在基体材料中的纤维组成的单向复合材料。其余四个由二维织物微观材料组成。这包括平织、4 综缎、5 综缎和 8 综缎复合材料。

对于任何微观结构，几何图形参数是构造逼真模型所必需的。对于单向材料，只需要单向复合材料的纤维体积因子 (FVF)。使用 FVF 并假定一个六边形纤维保压排列，为所需的复合材料开发微观力学模型的几何图形。但是，由于以下两个原因，织物纤维几何图形要复杂得多：

  1. 许多参数是描述单位单元的几何图形所必需的。
  2. 未使用任何通用数据集介绍平织的几何图形。

二维织物材料加入各种组合，如均衡平织、不均衡平织、斜织织物、缎纹编织等。Helius PFA 内使用的当前模型包括二维平织和 4 综缎、5 综缎和 8 综缎织物微观结构。对于仅包含正交牵引的其他织物配置（如斜纹编织），平织模型提供合理的估计，但是由您来决定结果的精度。因此，建议您计算层材料特性的上限，方法是将材料建模为跨层单向层压（其中每层都表示一个不同的牵引方向）。对于带有非正交牵引的微观结构（如三轴编织），Autodesk 当前不提供建模功能。

接下来的部分介绍使用 Helius PFA 实现的织物纤维微观结构，并将提供有关选择必要的参数来正确特征化织物材料的深入见解。

平织微观结构

平织复合材料微观力学模型由填充牵引、扭曲牵引和基体腔组成。假定填充和扭曲牵引互相垂直。为此类型的微观结构建模而选择的单位单元取自 Kuhn 和 Charalambides [1] ，如下所示。

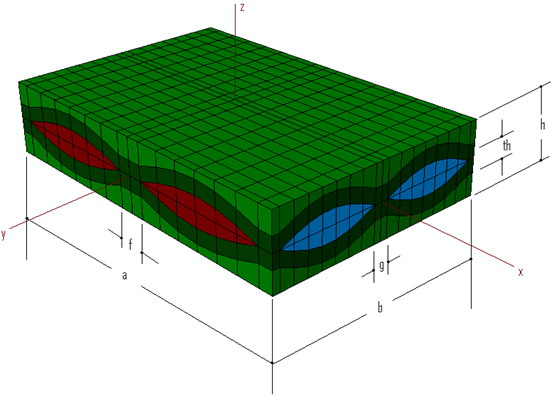
如上所示，完全描述单位单元的几何图形需要许多参数。这些步骤包括：

  1. 单位单元的长度
  2. 单位单元的宽度
  3. 单位单元的高度
  4. 填充迁移的高度
  5. 扭曲牵引的高度
  6. 填充牵引之间的间距
  7. 扭曲牵引之间的间距

没有基体腔的单位单元的视图如下所示。

完整单位单元微观结构（缎纹织物）

缎纹编织材料的完整单位单元 (FUC) 微观结构类似于平织模型，因为它由填充牵引、扭曲牵引和基体腔组成。FUC 还假设填充和扭曲牵引互相垂直。和平织微观结构一样，定义 FUC 微观结构也需要许多几何特性（长度、宽度、高度、间距）。

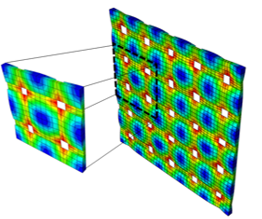
考虑到综缎数时，FUC 微观结构从平织模型的差异开始。随着我们从 4 进展到 5 再到 8 综缎材料，单位单元也开始增长。将新的牵引添加到微观结构以捕获每个缎纹类型各自的波动。下图描述了每个 n 综缎材料的微观结构（不显示各种束体积比例的基体腔）。请注意，单位单元的大小随着综缎数的增加而增加。

4 综缎

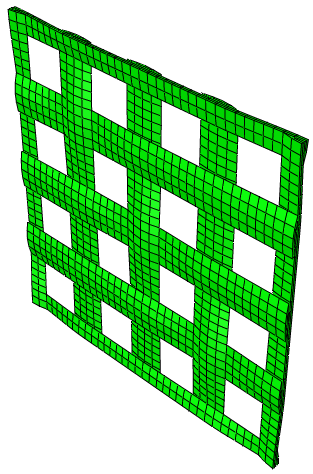
5 综缎

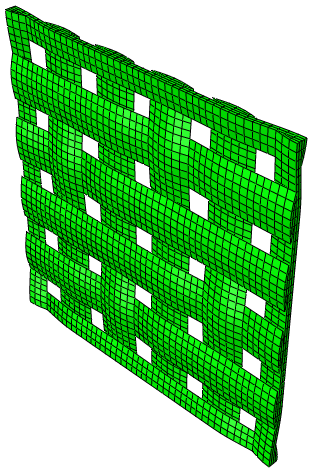
8 综缎

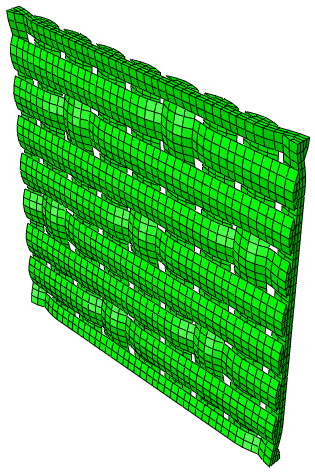
注： FUC 微观结构需要使用 Abaqus 针对损坏状态进行求解。不支持 FUC 微观结构的即时降级。

减少单位单元微观结构（缎纹编织）

缎纹编织材料的减少单位单元 (RUC) 微观结构是完整单位单元微观结构的改编。RUC 只是 FUC 中找到的重复几何图形的子集。RUC 保持恒定大小和拓扑，而不是针对每个 n 综缎材料调整微观结构。随着综缎数的变化，仅调整两个中心牵引的曲率的振幅。

具体而言，调整振幅以允许平均平面内刚度（E11、E22、G12）与每个综缎数的观察值实验性匹配。

RUC 微观结构具有小于 FUC 的独特结构，因此特征化速度很快。因此，RUC 微观结构支持纤维和基体刚度的即时降级。它还支持失效前非线性，但这在 FUC 中不受支持。

实验数据限制

纤维增强织物复合材料的实验数据通常仅特征化整个复合材料的纤维体积因子。和纤维增强单向复合材料一样，这为纤维在复合材料内占据的总体积（相对于复合材料的总体积）提供了测量。尽管这适用于单向材料，但这无法捕获织物微观结构的几何图形。为了将单位单元的几何图形与如下所述的参数关联，必须回答一个基础问题。什么是填充和扭曲牵引的体积因子？

若要回答此问题，我们必须先阐释体积因子之间的关系。复合材料的总纤维体积因子可以通过填充和扭曲牵引的体积因子以及它们各自的纤维体积因子描述为

FVF = BVFFill (FVFFill ) + BVFWarp (FVFWarp ) , (Eq. 1)

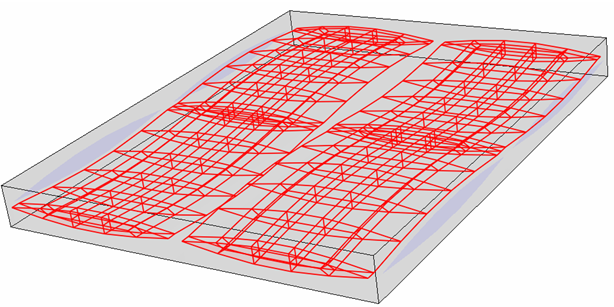
其中 BVFFill 是填充束体积因子，BVFWarp 是扭曲束体积因子，FVFFill 是填充牵引的纤维体积因子，而 FVFWarp 是扭曲牵引的纤维体积因子。束体积因子定义为指定牵引相对整个复合材料所占据的体积分数。若要提出有关束体积因子的更详细讨论及其在平织单位单元的几何图形上下文中的意义，请考虑下图。红色亮显区域表示填充牵引在整个复合材料单位单元中占据的体积。填充束体积因子的计算方式为填充牵引的体积除以复合材料的体积。

假设

此处我们对单位单元的几何图形进行一些假设。首先，我们假设填充和扭曲牵引相同，从而消除对两者高度的依存关系。第二个假设定义单位单元的总高度和牵引的高度在任何几何图形规范中都恒定。这可以有效消除上述列表中的第三个、第四个和第五个依存关系。

最后，我们假设牵引的宽度都相等且恒定。因此，单位单元的宽度和高度可能与牵引相关，如下所示：

a = width + 2f

b = width + 2g , (Eq. 2)

因此，需要两个未知参数才能完全描述单位单元的几何图形：填充牵引之间的间距和扭曲牵引之间的间距。这些参数与填充和扭曲束的体积因子以及每单位长度的波动数直接相关。Composite Material Manager 使用束体积因子 (BVF) 定义微观结构。

我们假设填充和扭曲束的纤维体积因子相等，从将 方程1 归纳为

FVF = (BVFFill + BVFWarp )FVFTow , (Eq. 3)

父主题： 附录 E：有关为织物材料文件指定几何图形的附加信息