粉末浓度模块采用“悬浮平衡模型”(SBM) 来预测粉末分离效果。
在此模型中,通常认为粒子法向应力梯度是粒子迁移的驱动力。因此,可以考虑剪切引起的粉末分离以及粉末浓度从上游到下游的对流。
SBM 将流体和粒子建模为两个阶段,但整个 Navier-Stokes 方程式仅针对流体和粒子混合或悬浮进行求解。将使用一个额外的粒子阶段质量平衡方程,它类似于传输方程。
在 Moldflow 中,SBM 模型由以下四个制约方程进行定义:
流体的质量守恒
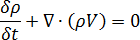 [1]
[1]
其中
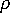 为悬浮密度
为悬浮密度
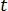 为时间
为时间
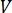 为速度矢量
为速度矢量
动量守恒
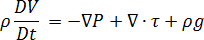 [2]
[2]
其中
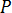 为压力
为压力
 为粘滞应力张量
为粘滞应力张量
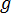 重力加速度矢量
重力加速度矢量
能量守恒
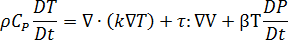 [3]
[3]
其中
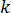 为热传导率
为热传导率
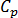 为比热容
为比热容
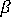 为膨胀率,定义如下
为膨胀率,定义如下
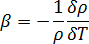
粒子阶段质量平衡
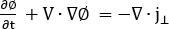 [4]
[4]
其中
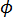 为粒子体积因子
为粒子体积因子
-
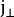 为粒子迁移通量,相对于 [5] 中定义的总体运动
为粒子迁移通量,相对于 [5] 中定义的总体运动
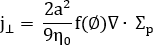 [5]
[5]
其中
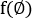 为沉积障碍函数
为沉积障碍函数
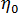 为悬浮流体粘度
为悬浮流体粘度
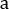 为粒子半径
为粒子半径
 为粒子法向应力,在 [6] 中进行定义
为粒子法向应力,在 [6] 中进行定义
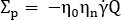 [6]
[6]
其中
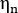 为粒子法向应力粘度,在 [7] 中进行定义
为粒子法向应力粘度,在 [7] 中进行定义
- 张量
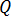 定义法向应力的各向异性,在 [8] 中进行定义
定义法向应力的各向异性,在 [8] 中进行定义
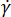 为剪切速率,在 [9] 中进行定义
为剪切速率,在 [9] 中进行定义
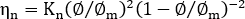 [7]
[7]
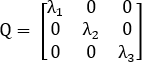 [8]
[8]
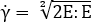 [9]
[9]