Überprüfen Sie die Auswirkungen der nichtlinearen Längsscherreaktion von Verbundmaterialien.
Vor dem endgültigen Versagen weisen Verbundwerkstoffe typischerweise eine sehr geringe Nichtlinearität bei der normalen Spannungs-/Dehnungsreaktion auf. Sie weisen jedoch in der Regel eine erhebliche Nichtlinearität bei der Scherspannungs-/-dehnungsreaktion vor dem endgültigen Versagen auf. Diese Nichtlinearität ist besonders stark bei der Längsscherreaktion (d. h.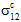 
im Vergleich zu 
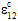und 
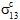im Vergleich zu 
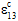) ausgeprägt.
Es wird davon ausgegangen, dass die Quelle des nichtlinearen Längsscherverhaltens des Verbundmaterials die Anhäufung von Submikrorissen in der Matrixkonstituente ist, während die Faserkonstituente unbeschädigt bleibt. Außerdem wird davon ausgegangen, dass die Anhäufung von Submikrorissen in der Matrixkonstituente zu einer progressiven Degradation des Längsschermoduls der Matrixkonstituente und einer entsprechenden progressiven Degradation des Längsschermoduls des Verbundmaterials führt, ohne Auswirkungen auf die restlichen Verbund- oder Konstituentenmodule.
Bei Situationen, in denen dieses nichtlineare Längsscherverhalten wichtig für Sie ist, bietet Helius PFA eine Funktion für Nichtlinearität vor Ausfall, die eine Abschwächung der nichtlinearen Längsscherung in die Reaktion sowohl der Matrixkonstituente als auch des Verbundmaterials integriert. Aus Gründen der Berechnungszweckmäßigkeit und algorithmischen Einfachheit wird die Degradation der durchschnittlichen Längsschermodule der Matrix (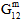
und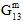 
) und der durchschnittlichen Längsschermodule des Verbundwerkstoffs (
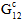und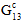 
) nicht als kontinuierliche Degradation modelliert. Vielmehr wird sie über eine Reihe von diskreten Reduktionen auferzwungen, die vor der Erkennung des Matrixkonstituentenversagens auftreten (daher der Name Nichtlinearität vor Ausfall). Drei diskrete Reduktionen werden auf unidirektionale Verbundwerkstoffe und sechs diskrete Reduktionen auf gewebte Verbundwerkstoffe angewendet. Es sollte betont werden, dass jede einzelne Reduktion bei den durchschnittlichen Längsschermodulen der Matrix ( 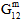und 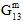) (im Sinne der MCT) zur diskreten Reduktion bei den durchschnittlichen Längsschermodulen des Verbundwerkstoffs ( 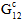und 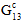) konsistent sein muss, da die Verbundeigenschaften durch Homogenisierung der heterogenen Mikrostruktur erreicht werden.
Um optimale Voraussetzungen für die Beschreibung der Implementierung der Funktion für Nichtlinearität vor Ausfall zu schaffen, sehen Sie sich Teil A des Diagramms im Abschnitt Schadenszustände in unidirektionalen Verbundmaterialien an. Konzentrieren Sie sich auf den linearen elastischen Bereich (mit der Bezeichnung Schadenszustand 1) am Anfang, der vor einem Matrix- oder Faserkonstituentenversagen auftritt. Wie bereits erwähnt, ist ein lineares elastisches Verhalten vor Matrixausfällen für normale Spannungen vertretbar. Die Längsschersteifheit eines Verbundmaterials sollte eine beträchtliche Abschwächung vor dem Matrixversagen aufweisen.
Unidirektionale Verbundwerkstoffe
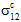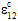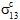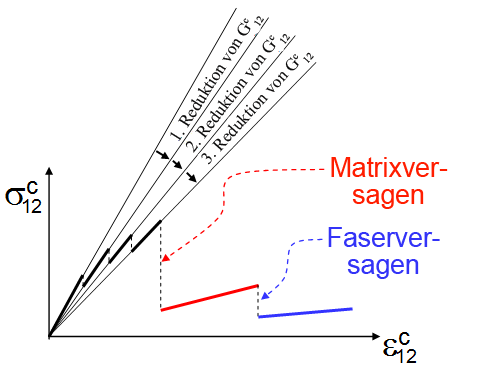
Im Bereich mit der Bezeichnung "Schadenszustand 1" in Teil A des oben genannten Diagramms verwendet die Funktion für Nichtlinearität vor Ausfall in Helius PFA eine Darstellung der Längsscherreaktion aus vier Segmenten mit abschnittsweiser Linearität (also im Vergleich zu und im Vergleich zu 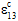). Die ursprüngliche lineare elastische Reaktion für die übrigen vier Spannungs- und Dehnungskomponenten bleibt erhalten. 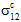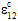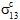Das Diagramm unten stellt eine qualitative Veranschaulichung der durchschnittlichen Längsscherreaktion des unidirektionalen Verbundwerkstoffs ( im Vergleich zu und im Vergleich zu 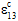) dar, die auftritt, wenn die Funktion für Nichtlinearität vor Ausfall in Helius PFA aufgerufen wird. In diesem Diagramm durchlaufen die durchschnittlichen Längsschermodule des Verbundwerkstoffs ( 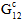und 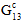) vor einem Matrix- oder Faserkonstituentenversagen eine Reihe von drei diskreten Reduktionen. 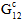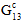Die einzelnen Reduktionen in und werden vollständig durch konsistente diskrete Reduktionen in den durchschnittlichen Längsschermodulen 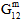und 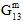erzeugt, während alle anderen Matrix- und Faserkonstituenteneigenschaften konstant bleiben. Diese Vorgehensweise dient zum Simulieren der graduellen Anhäufung von Submikrorissen in der Matrix, die vor dem vollständigen Matrixscherversagen auftritt.
Gewebte Verbundwerkstoffe
Im Bereich mit der Bezeichnung "Schadenszustand 1" in Teil A des oben genannten Diagramms verwendet die Funktion für Nichtlinearität vor Ausfall in Helius PFA eine Darstellung der Längsscherreaktion aus sieben Segmenten mit abschnittsweiser Linearität (also 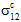im Vergleich zu 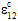und 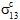im Vergleich zu 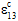). Die ursprüngliche lineare elastische Reaktion für die übrigen vier Spannungs- und Dehnungskomponenten bleibt erhalten. 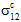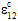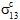Das Diagramm unten stellt eine qualitative Veranschaulichung der durchschnittlichen Längsscherreaktion des gewebten Verbundwerkstoffs ( im Vergleich zu und im Vergleich zu 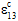) dar, die auftritt, wenn die Funktion für Nichtlinearität vor Ausfall in Helius PFA aufgerufen wird. In diesem Diagramm durchlaufen die durchschnittlichen Längsschermodule des Verbundwerkstoffs ( 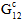und 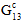) vor einem Matrix- oder Faserkonstituentenversagen eine Reihe von sechs diskreten Reduktionen. 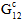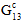Die einzelnen Reduktionen in und werden vollständig durch konsistente diskrete Reduktionen in den durchschnittlichen Längsschermodulen 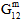und 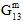erzeugt, während alle anderen Matrix- und Faserkonstituenteneigenschaften konstant bleiben. Diese Vorgehensweise dient zum Simulieren der graduellen Anhäufung von Submikrorissen in der Matrix, die vor dem vollständigen Matrixscherversagen auftritt.
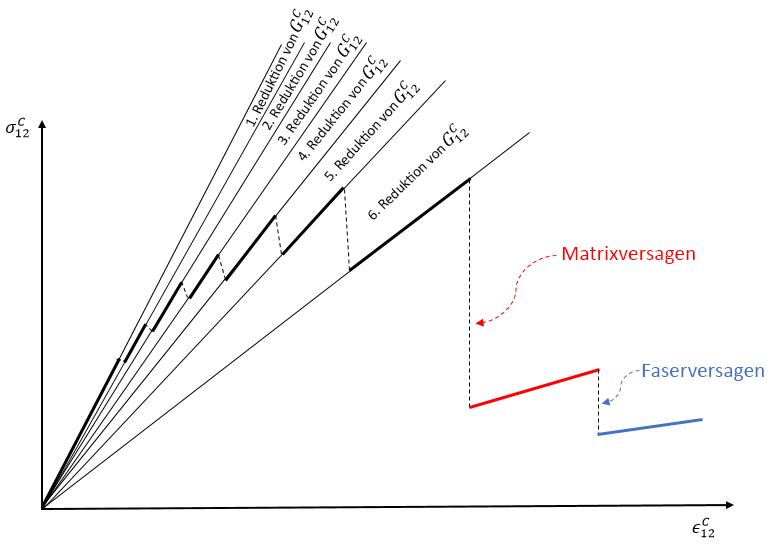
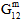und 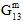und die Ebenen der durchschnittlichen Längsscherspannung der Matrix (
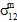und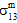 
) bezeichnen, denen diese Reduktionen aufgezwungen werden. Logischerweise erfordert die Bestimmung dieser Konstanten eine gemessene Längsscherspannungs-/-dehnungskurve (z. B. 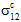im Vergleich zu 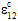) für das fragliche Verbundmaterial. Es sollte betont werden, dass das Aufrufen dieser Funktion nicht die Scherspannungsebene ändert, auf der das Matrixversagen auftritt. Es wird dadurch allerdings das Ausmaß der Scherverformung erhöht, das vor dem Matrixversagen auftritt.