Das Wärmestrahlungsmodell kann die Auswirkungen des temperaturabhängigen Emissionsvermögens berücksichtigen. Dies ermöglicht die Simulation der Wirkungen von spektraler Strahlung. Die entsprechende Variation muss in Form einer stückweise linearen Tabelle verfügbar sein und wird im Materialeditor eingegeben, indem Sie auf die Schaltfläche "Emissionsvermögen" klicken und "Stückweise linear" aus der Dropdown-Liste "Variationsmethode" wählen.
Um die spektralen Eigenschaften einer Fläche zu berücksichtigen, konstruieren Sie mithilfe der Strahlungsfunktionen in der folgenden Tabelle eine zweite Tabelle des gesamten Emissionsvermögens als Funktion der Temperatur zur Verwendung in Autodesk® CFD:
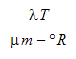
|
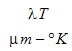
|
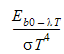
|
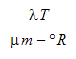
|
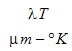
|
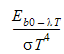
|
| 0 | 0 | 0.0 | 10,200 | 5666.7 | 0.70754 |
| 1000 | 555.6 | 1.70e-8 | 10,400 | 5777.8 | 0.71806 |
| 1200 | 666.7 | 7.56e-7 | 10,600 | 5888.9 | 0.72813 |
| 1400 | 777.8 | 1.06e-5 | 10,800 | 6000 | 0.73777 |
| 1600 | 888.9 | 7.38e-5 | 11,000 | 6111.1 | 0.74700 |
| 1800 | 1000 | 3.21e-4 | 11,200 | 6222.2 | 0.75583 |
| 2000 | 1111.1 | 0.00101 | 11,400 | 6333.3 | 0.76429 |
| 2200 | 1222.2 | 0.00252 | 11,600 | 6444.4 | 0.77238 |
| 2400 | 1333.3 | 0.00531 | 11,800 | 6555.6 | 0.78014 |
| 2600 | 1444.4 | 0.00983 | 12,000 | 6666.7 | 0.78757 |
| 2800 | 1555.6 | 0.01643 | 12,200 | 6777.8 | 0.79469 |
| 3000 | 1666.7 | 0.02537 | 12,400 | 6888.9 | 0.80152 |
| 3200 | 1777.8 | 0.03677 | 12,600 | 7000 | 0.80806 |
| 3400 | 1888.9 | 0.05059 | 12,800 | 7111.1 | 0.81433 |
| 3600 | 2000 | 0.06672 | 13,000 | 7222.2 | 0.82035 |
| 3800 | 2111.1 | 0.08496 | 13,200 | 7333.3 | 0.82612 |
| 4000 | 2222.2 | 0.10503 | 13,400 | 7444.4 | 0.83166 |
| 4200 | 2333.3 | 0.12665 | 13,600 | 7555.6 | 0.83698 |
| 4400 | 2444.4 | 0.14953 | 13,800 | 7666.7 | 0.84209 |
| 4600 | 2555.6 | 0.17337 | 14,000 | 7777.8 | 0.84699 |
| 4800 | 2666.7 | 0.19789 | 14,200 | 7888.9 | 0.85171 |
| 5000 | 2777.8 | 0.22285 | 14,400 | 8000 | 0.85624 |
| 5200 | 2888.9 | 0.24803 | 14,600 | 8111.1 | 0.86059 |
| 5400 | 3000 | 0.27322 | 14,800 | 8222.2 | 0.86477 |
| 5600 | 3111.1 | 0.29825 | 15,000 | 8333.3 | 0.86880 |
| 5800 | 3222.2 | 0.32300 | 16,000 | 8888.9 | 0.88677 |
| 6000 | 3333.3 | 0.34734 | 17,000 | 9444.4 | 0.90168 |
| 6200 | 3444.4 | 0.37118 | 18,000 | 10,000 | 0.91414 |
| 6400 | 3555.6 | 0.39445 | 19,000 | 10,555.6 | 0.92462 |
| 6600 | 3666.7 | 0.41708 | 20,000 | 11,111.1 | 0.93349 |
| 6800 | 3777.8 | 0.43905 | 21,000 | 11,666.7 | 0.94104 |
| 7000 | 3888.9 | 0.46031 | 22,000 | 12,222.2 | 0.94751 |
| 7200 | 4000 | 0.48085 | 23,000 | 12,777.8 | 0.95307 |
| 7400 | 4111.1 | 0.50066 | 24,000 | 13,333.3 | 0.95788 |
| 7600 | 4222.2 | 0.51974 | 25,000 | 13,888.9 | 0.96207 |
| 7800 | 4333.3 | 0.53809 | 26,000 | 14,444.4 | 0.96572 |
| 8000 | 4444.4 | 0.55573 | 27,000 | 15,000 | 0.96892 |
| 8200 | 4555.6 | 0.57267 | 28,000 | 15,555.6 | 0.97174 |
| 8400 | 4666.7 | 0.58891 | 29,000 | 16,111.1 | 0.97423 |
| 8600 | 4777.8 | 0.60449 | 30,000 | 16,666.7 | 0.97644 |
| 8800 | 4888.9 | 0.61941 | 40,000 | 22,222.2 | 0.98915 |
| 9000 | 5000 | 0.63371 | 50,000 | 27,777.8 | 0.99414 |
| 9200 | 5111.1 | 0.64740 | 60,000 | 33,333.3 | 0.99649 |
| 9400 | 5222.2 | 0.66051 | 70,000 | 38,888.9 | 0.99773 |
| 9600 | 5333.3 | 0.67305 | 80,000 | 44,444.4 | 0.99845 |
| 9800 | 5444.4 | 0.68506 | 90,000 | 50,000 | 0.99889 |
| 10,000 | 5555.6 | 0.69655 | 100,000 | 55,555.6 | 0.99918 |
Bestimmen Sie das Emissionsvermögen aus den Werten in dieser Tabelle mithilfe der folgenden Gleichung:
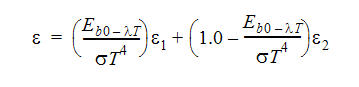
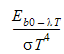 ist die dimensionslose Schwarzkörper-Strahlungsleistung.
ist die dimensionslose Schwarzkörper-Strahlungsleistung.
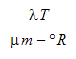 ist die spektrale Temperatur (einschließlich Einheiten).
ist die spektrale Temperatur (einschließlich Einheiten).
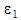 ist die Ausstrahlung bei Wellenlängen unter 3
ist die Ausstrahlung bei Wellenlängen unter 3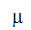 .
.
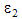 ist die Ausstrahlung bei größeren Wellenlängen (über 3
ist die Ausstrahlung bei größeren Wellenlängen (über 3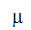 ).
).
Beispiel:
- Der Temperaturbereich in einem Modell liegt zwischen100 °F und 1200 °F.
-
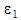 = 0.3.
= 0.3. -
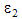 = 0.8.
= 0.8.
Um die spektrale Temperatur bei 100 °F zu ermitteln, multiplizieren Sie die Wellenlänge (3) mit der Temperatur in absoluten Einheiten (560 R). Um die dimensionslose Schwarzkörper-Strahlungsleistung zu ermitteln, verwenden Sie die obige Tabelle zum Interpolieren des Werts für die berechnete spektrale Temperatur:
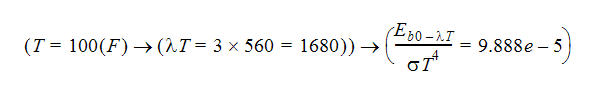
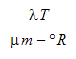
|
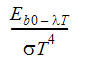
|
| 1680 | 9.888e-5 |
Das Emissionsvermögen bei 100 °F ergibt sich wie folgt:
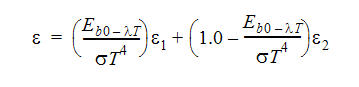
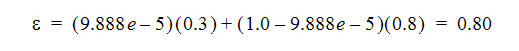
Um die spektrale Temperatur bei 1200 °F zu ermitteln, multiplizieren Sie die Wellenlänge (3) mit der Temperatur in absoluten Einheiten (1660 R). Um die dimensionslose Schwarzkörper-Strahlungsleistung zu ermitteln, verwenden Sie die obige Tabelle zum Interpolieren des Werts für die berechnete spektrale Temperatur:
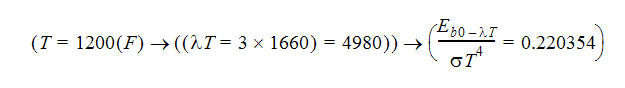
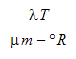
|
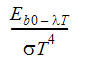
|
| 4980 | 0.220354 |
Das Emissionsvermögen bei 1200 °F ergibt sich wie folgt:
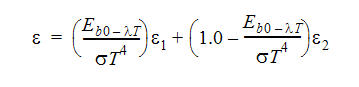
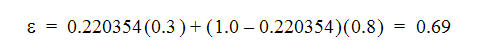
Geben Sie das Emissionsvermögen und die Temperaturwerte in eine Eigenschaftstabelle vom Typ "Stückweise linear" im Materialeditor ein:
| Emissionsvermögen | Temperatur (F) |
| 0.8 | 100 |
| 0.69 | 1200 |