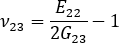Fiber orientation is one of the major factors that determines the mechanical (elastic) strength as well as the stiffness of a molded part.
Theories have been developed to predict the mechanical properties of short fiber composites once the fiber orientation distribution in the parts is known.
To calculate the mechanical properties, all the theories follow a two step procedure:
- The properties of a unidirectional short fiber reinforced material are estimated.
- These properties are then averaged according to the fiber orientation distribution.
Thus, this methodology independently accounts for the influence of fiber length and fiber orientation.
The Tandon-Weng model serves as the basis for the calculation of the composite material's unidirectional mechanical properties for an isotropic matrix. The Autodesk Moldflow Insight implementation also considers Tucker/Liang's treatment on the Poisson ratio calculation of the Tandon-Weng model.
The properties of the fiber and polymer required as inputs to the analysis are:
-
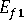(longitudinal modulus of fiber)
-
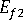(transverse modulus of fiber)
-
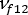(longitudinal Poisson's ratio of fiber)
-
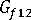(longitudinal shear modulus of fiber)
-
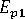(longitudinal modulus of polymer)
-
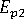(transverse modulus of polymer)
-
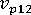(longitudinal Poisson's ratio of polymer)
-
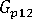(longitudinal shear modulus of polymer)
-
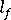(average fiber length)
-
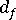(average fiber diameter)
-
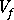(volume fraction of fibers)
The following basic mechanical properties are derived for each element in the composite material:
-
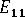(longitudinal modulus)
-
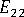(transverse modulus)
-
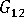(in-plane shear modulus)
-
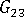(out-of-plane shear modulus)
-
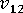(in-plane Poisson's ratio)
-
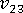(out-of-of-plane Poisson's ratio)
Longitudinal and transverse moduli
The Tandon-Weng model treats the short fiber reinforced composite as a special case of unidirectionally aligned spheroidal inclusions embedded in a finite elastic polymer matrix.
The longitudinal modulus of the uniaxially aligned system can be written as:
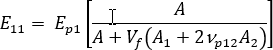
where
,
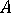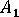and 
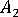are parameters related to those in the Tandon Weng paper.
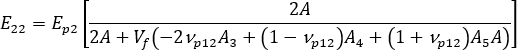
where ,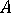 
, 
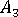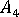and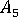 
are parameters related to those in Tandon and Weng's paper.
Shear moduli and Poisson's ratios
The longitudinal shear modulus of the uniaxially aligned system can be written as:
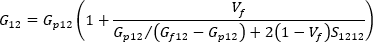
and the transverse shear modulus of the uniaxially aligned system can be written as:
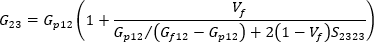
where S1212 and S2323 are the corresponding components of Eshelby's tensor, the analytical solution of which is presented in Tandon and Weng's paper.
The in-plane Poisson's ratio of the uniaxially aligned system can be written as:
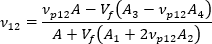
The out-of-plane Poisson's ratio of the uniaxially aligned system can be explicitly calculated from the composite moduli as:
