繊維配向は、成形品の機械的(弾性)強度と剛性を決定する、主な要素の 1 つです。
成形品における繊維配向の分布が明らかになって以来、短繊維複合材料の機械的特性を予測する各種理論が開発されてきました。
どの理論でも、機械的特性を計算するために、次の 2 手順の手順に従います。
- 一方向短繊維強化材料のプロパティを見積もります。
- その後これらのプロパティは、繊維配向の分布に基づいて平均化されます。
このように、この方法論では、繊維の長さと配向の影響が単独で説明されます。
Tandon-Weng モデルは、等方性マトリックスの複合材料の一方向機械的特性を計算する基礎になります。Autodesk Moldflow Insight の実装では、Tandon-Weng モデルのポアソン比計算に対する Tucker/Liang の扱いも考慮しています。
解析で入力が必要なファイバーおよび樹脂のプロパティは、次のとおりです。
-
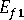 (ファイバーの縦弾性率)
(ファイバーの縦弾性率)
-
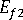 (ファイバーの横弾性率)
(ファイバーの横弾性率)
-
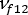 (ファイバーの縦ポアソン比)
(ファイバーの縦ポアソン比)
-
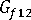 (ファイバーの縦せん断弾性率)
(ファイバーの縦せん断弾性率)
-
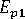 (樹脂の縦弾性率)
(樹脂の縦弾性率)
-
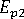 (樹脂の横弾性率)
(樹脂の横弾性率)
-
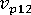 (樹脂の縦ポアソン比)
(樹脂の縦ポアソン比)
-
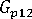 (樹脂の縦せん断弾性率)
(樹脂の縦せん断弾性率)
-
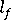 (平均ファイバー長)
(平均ファイバー長)
-
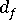 (平均ファイバー直径)
(平均ファイバー直径)
-
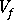 (ファイバーの体積率)
(ファイバーの体積率)
次の基本機械的特性は、複合材料の要素ごとに定義されます。
-
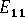 (縦弾性率)
(縦弾性率)
-
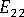 (横弾性率)
(横弾性率)
-
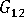 (面内せん断弾性率)
(面内せん断弾性率)
-
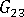 (面外せん断弾性率)
(面外せん断弾性率)
-
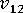 (面内ポアソン比)
(面内ポアソン比)
-
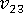 (面外ポアソン比)
(面外ポアソン比)
縦弾性率および横弾性率
Tandon-Weng モデルでは、短繊維強化複合材料は、有限弾性樹脂マトリックスに組み込まれた、一方向に整列した楕円体含有物近似の特殊ケースとして扱われます。
一軸整列システムの縦弾性率は、次のように記述することができます。
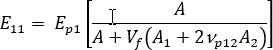
説明: 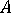 ,
, 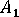 および
および 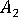 は、Tandon Weng の論文で使用されているパラメータに関連するパラメータです。
は、Tandon Weng の論文で使用されているパラメータに関連するパラメータです。
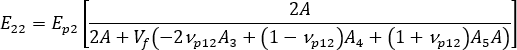
ここで、 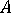 ,
, 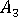 ,
, 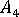 、および
、および 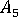 は Tandon および Weng の論文にあるものに関連するパラメータです。
は Tandon および Weng の論文にあるものに関連するパラメータです。
せん断弾性率およびポアソン比
一軸整列システムの縦せん断弾性率は、次のように記述することができます。
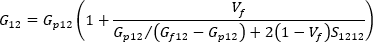
また、一軸整列システムの横せん断弾性率は、次のように記述することができます。
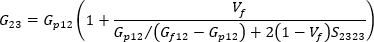
ここで、S1212 および S2323 は Eshelby のテンソルの対応コンポーネントであり、その解析ソリューションは Tandon および Weng の論文に記述されています。
一軸整列システムの面内ポアソン比は、次のように記述できます。
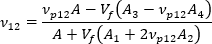
一軸整列システムの面外ポアソン比は、複合材料係数から次のように明示的に計算することができます。