分布抵抗モデル

解析特性

• 定常状態
• 3 次元内部流れ
• 乱流
• 非圧縮性流れ
• 分布抵抗モデル

参考文献

White,F.M., ﾒFluid Mechanicsﾓ, McGraw-Hill, New York, 1979, pp. 305-360305-360

Idelchik, I.E., ﾒHandbook of Hydraulic Resistanceﾓ, CRC Press, 1994, pp. 523523

問題の説明

流路の中央にフィルタまたはいくつかの障害物の存在するスリップ壁が定義された 3 次元流路があり、この中を空気が流れています。流路全体の圧力損失は、壁にスリップ条件が存在するため、障害物によってのみ引き起こされます。

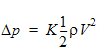
4つの分布抵抗モデルの全てをテストします。

1. 一定抵抗係数 K:

K = 1.97748

指定した圧力損失では、この抵抗係数 K により流量が 0.2 m3/s になります。

2. 管摩擦損失:

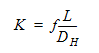
ここで、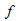 は摩擦係数です。この係数を得るために摩擦係数に関するブラシウスの式を使用します。L = 41.99 はパイプの長さで、DH = 0.2 はパイプの水力直径です。摩擦係数を得るためのブラシウスの式は次の通りです：

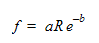
ここで、a は 0.316、b は 0.25 です。これらの値により、1.97748 と同等の抵抗係数 K が得られます。ここで、流量は 0.2 m³/s とみなすことができます。

3. 開口面積比

この抵抗タイプについては、Idelchik著の参考文献516ページに記載されている式を使用します：

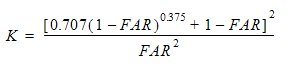
ここで、FAR は開口面積比です。開口面積が 0.62 の場合、抵抗係数 K は 1.9774 となり、したがって流量は 0.2 m³/s になります。

4. 圧力損失係数 K:

下表の値を使用します：

流量(m3/sec)	圧力ヘッド(Pa)
0.15	35000
0.25	45000

ジオメトリと境界条件

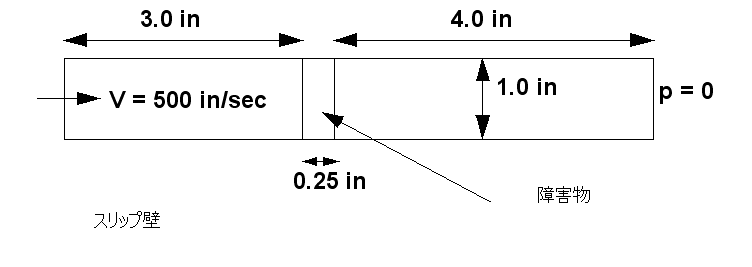
結果

分布抵抗のモデル	ベンチマーク	2018: ビルド 20170308	誤差 %	2019: ビルド 20180130	誤差 %
定数 K	0.2 m3/s	0.1997	0.143	0.1961	1.95
管摩擦損失	0.2 m3/s	0.2171	8.569	0.1982	.896
開口面積比	0.2 m3/s	0.1997	0.143	0.1961	1.95
水頭損失テーブル	0.2 m3/s	0.1979	1.0475	0.1999	.004