Curvas e superfícies NURBS não existem no mundo de desenho tradicional. Foram criadas especificamente para modelo 3D usando computadores. Curvas e superfícies representam contornos ou formas dentro de um espaço de modelo 3D. Elas são construídas matematicamente.
A matemática do NURBS é complexa, e esta seção é simplesmente uma introdução para alguns conceitos de NURBS que podem ajudá-lo a compreender o que você está criando, e por que os objetos de NURBS se comportam de tal maneira. Para obter uma descrição completa da matemática e dos algoritmos envolvidos no modelo de NURBS, consulte The NURBS Book por Les Piegl e Wayne Tiller (Nova York: Springer, Segunda edição 1997 ).
Definição e Espaço de Parâmetro
O termo NURBS significa Non-Uniform Rational B-Splines. Especificamente:
- Non-Uniformsignifica que a extensão da influência de um vértice de controle pode variar. Isto é útil ao modelar superfícies irregulares.
- Rational significa que a equação usada para representar a curva ou superfície é expressa como um coeficiente de dois polinômios de, ao invés de um único polinômio somado. A equação racional fornece um modelo melhor de algumas curvas e superfícies importantes, especialmente seções cônicas, cones, esferas, e assim por diante.
- B-spline(para spline de base) é uma forma de criar uma curva que é intercalada entre três ou mais pontos.
Curvas de forma, como a ferramenta Line (linha) e outras ferramentas Shape (forma) são curvas Bezier, que é um caso especial de B-splines.
A propriedade não uniforme de NURBS traz um ponto importante. Por serem gerados matematicamente, os objetos NURBS têm um parâmetro espaço de parâmetro junto com o espaço geométrico 3D em que são exibidos. Especificamente, uma matriz de valores denominada nós especifica a extensão de influência de cada vértice de controle (control vertex - CV) na curva ou superfície. Os nós são invisíveis no espaço 3D e você não pode manipulá-los diretamente, mas ocasionalmente seu comportamento afeta a aparência visível do objeto NURBS. Este tópico menciona essas situações. O espaço do parâmetro é unidimensional para curvas, que têm apenas uma única dimensão U topologicamente, mesmo se existirem geometricamente no espaço 3D. As superfícies têm duas dimensões no espaço do parâmetro, chamadas de U e V.
Curvas e superfícies NURBS têm propriedades importantes de não alterar sob a as transformações afins geométricas padrão (transformações), ou em projeções em perspectiva. Os CVs têm controle local do objeto: mover um CV ou alterar seu peso não afeta qualquer parte do objeto para além dos CVs vizinhos. (é possível modificar esta propriedade utilizando os controles Seleção Suave). Além disso, a retícula de controle que conecta o CVs circunda a superfície. Isto é conhecido como propriedade de cobertura convexa.
Grau e continuidade
Todas as curvas têm um grau. O grau de uma curva é o maior expoente na equação usada para representá-lo. Uma equação linear de grau 1; uma equação quadrática é grau 2. As curvas NURBS normalmente são representadas por equações cúbicas e têm um grau de 3. Graus maiores são possíveis, mas normalmente desnecessários.
As curvas também têm continuidade. Uma curva contínua não é quebrada. Há diferentes níveis de continuidade. Uma curva com um ângulo ou cúspide é C 0 contínua: ou seja, a curva é contínua, mas não possui derivativa no cúspide. Uma curva sem cúspide, mas cujas alterações de curvatura sejam 1 contínuas. Sua derivativa também é contínua, mas sua segunda derivativa não é. Uma curva com uma curvatura ininterrupta e inalterável é 2 contínua. As primeiras e segundas derivativas também são contínuas.

Níveis de continuidade da curva:
Esquerda: C 0 , porque o ângulo no topo
Meio: C 1 na parte superior de um semicírculo une um semicírculo de menor raio
Direita: C 2 , a diferença é sutil, mas o lado direito não é semicircular e mescla com o esquerdo
Uma curva pode ter ainda maiores níveis de continuidade, mas para modelo de computador, essas três são adequadas. Normalmente os olhos conseguem distinguir entre uma curva contínua de C 2 e uma com continuidade maior.
Continuidade e grau estão relacionados. Uma equação de grau 3 pode gerar uma curva contínua C 2 . Esta é a razão pela qual as curvas de grau superior não são geralmente necessárias em modelagem NURBS. Curvas de grau superior também são menos estáveis numericamente, portanto, não é recomendado utilizá-las.
Diferentes segmentos de uma curva NURBS podem ter diferentes níveis de continuidade. Em particular, colocando os CVs na mesma localização ou muito próximos, você reduz a continuidade de nível. Dois coincidente VCs afiar a curvatura. Três CVs coincidentes criam um cúspide angular na curva. Esta propriedade de curvas de NURBS é conhecida como multiplicidade. Em efeito, o um ou dois CVs adicionais combinam sua influência na proximidade da curva.
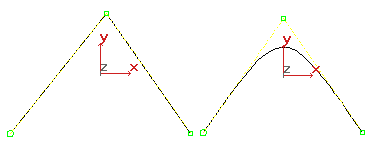
Efeitos de multiplicidade: há três CVs no vértice à esquerda, dois CVs no vértice à direita.
Ao mover um CV para longe uns dos outros, você aumenta a continuidade da curva de nível novamente. A multiplicidade também se aplica ao fundir os CVs. Os CVs fundidos criam uma curvatura mais aguda ou um cúspide na curva. Novamente, o efeito desaparecerá se você desfundir os CVs e remover um do outro.
Grau, continuidade e multiplicidade de aplicar às superfícies NURBS, bem como para curvas.
Refinar as curvas e superfícies
Refinamento uma curva NURBS significa adicionar mais CVs. Refinar oferece maior controle sobre a forma da curva. Ao refinar uma curva NURBS, o 3ds Max preserva a curvatura original. Em outras palavras, a forma da curva não é alterada, mas os CVs que ao redor movem o CV que você adicionou. Isto é por causa da multiplicidade: se os CVs próximos não forem movidos, o aumento de presença de CVs formaria a curva. Para evitar este efeito, primeiro efetue o refinamento da curva e, a seguir, altere a transformação recém adicionada de CVs ou ajuste seus pesos.
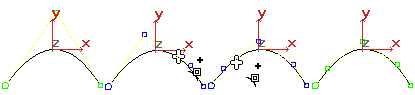
Refinar uma curva NURBS
As superfícies NURBS têm basicamente a mesma propriedades que as curvas NURBS, estendidas de um espaço de parâmetro unidimensional para dois dimensionais.
Reparametrização de curvas CV e superfícies
Ao efetuar o refinamento de uma curva ou superfície NURBS, é uma boa ideia reparameterizá-la. A reparametrização ajusta o espaço de parâmetros para a curva ou superfície que irá se comportar bem quando ao editar nas viewports. Há duas maneiras de reparametrização:
- Comprimento do banzo
Os nós dos espaços de reparametrização do comprimento do banzo no espaço de parâmetro baseado na raiz quadrada do comprimento de cada segmento de curva.
- Uniforme
Os espaços de reparemetrização uniforme têm nós uniformes. Um vetor de nó uniforme tem a vantagem de que a curva ou a superfície é alterada apenas localmente quando é editada.
A curva CV e os subobjetos de superfície dão a opção de reparemetrização automaticamente sempre que você editar a curva ou superfície.
Conceitos de curva de ponto e superfície
É possível trabalhar com curvas e superfícies, bem como com curvas CV e superfícies. Os pontos que controlam esses objetos são restringidos para estarem na curva ou superfície. Não há nenhuma retícula de controle e nenhum controle de peso. Esta é uma interface simples que você pode achar mais fácil de trabalhar. Também, objetos com base em ponto fornecem a habilidade de criar curvas com base em pontos dependentes (restringidos) e, a seguir, usam estes para criar superfícies dependentes.
Você pode considerar curvas de pontos e superfícies como uma interface para as curvas e superfícies CV, que são os objetos NURBS completamente definidos. A representação subjacente da curva ou superfície ainda é construída usando CVs.
Você pode considerar um ponto de curva ou superfície como dependente em seus pontos. É possível utilizar o botão Converter Curva para converter uma curva de ponto ou superfície para a forma do CV, ou vice-versa.