乱流

乱流ダイアログでは、乱流の有効化または無効化、乱流モデルの選択、乱流モデルのパラメータの変更を行います。

層流をシミュレートするには、層流を選択します。

乱流をシミュレートするには、乱流（デフォルト）を選択します。通常、工学的な流れは乱流である場合が多いといえます。

解析を層流または乱流として実行するべきかが不確かである場合は、まず層流を試してみてください。流れが実際に乱流である場合、一般的に解析は最初の10回から15回の収束計算において発散します。設定を乱流に変更し、収束計算数0から再び開始します。

乱流モデル

次の表に、使用可能な乱流モデル、その推奨される用途、およびいくつかの追加情報を示します。

乱流モデル	推奨される使用	注
k-ε	ほとんどのアプリケーションで正常に動作します	汎用の乱流モデル既定のモデル
SST k-ω	外部空気力学: 分離または剥離された流れ逆圧勾配を持つ流れ	SST は壁関数を使用する代わりに、壁までの乱流をシミュレートします。境界層領域ではメッシュを非常に細かくする必要があります。 [壁レイヤ]ダイアログでは最大 10 のレイヤを追加できます。詳細については、以下の注意事項を参照してください。
SST k-ω SAS (スケールアダプティブシミュレーション)	以下のような、非定常乱流構造を持つ流れ。渦の離脱可変の後流構造	SST k-ω SAS で定常シミュレーションを実行することができます。乱流構造をアニメーション化することはできませんが、このモデルでは、定常 k-εシミュレーションよりも適切にモデルの形成および形状を予測します。境界層領域ではメッシュを非常に細かくする必要があります。[壁レイヤ]ダイアログでは最大 10 のレイヤを追加できます。
SST k-ω RC (Smirnov-Menter)	一般にサイクロンセパレータに見られるような曲率の高いフロー。	これは回転および曲率(RC)補正を備えた Menter の 2 方程式モデルです。このモデルでは多くの計算が実行され、また細かいメッシュが必要となります。場合によっては、このモデルでは収束のために数千回の反復が必要になることがあります。
SST k-ω RC (Hellsten)	特定の翼には NACA0012 と Coanda 翼が含まれます。小型で高速回転する装置曲がりの大きなフローや凸面上のフロー	これは、Hellsten の単純化された回転/曲率補正を備えた Menter SST の 2 方程式モデルです。分離ポイントを他の乱流モデルでは予測するのが難しい凸型サーフェスでのフロー予測に役立ちます。
SST k-ω DES (剥離エディシミュレーション)	分離された高いレイノルズ数の外部空気力学の流れ。	これは、SST k-ω とラージエディシミュレーション(LES)モデルを組み合わせたものです。このモデルでは多くの計算が必要です。また、メッシュ分布に敏感です。これは均一なメッシュ分布で最適に動作します。
RNG	個別の流れ(特に後方ステップでの流れ)に対する再付着点。	多くの計算を必要としますが、k-ε モデルよりわずかに正確な場合があります。最初に k-ε モデルを使用して開始し、流れがほぼ収束してから RNG に切り替えることをお勧めします。
低 Re k-ε	レイノルズ数の範囲が 1,500 から 5,000 の低速の乱流。低速と高速の両方の領域を持つ流れ。層流から乱流に遷移するパイプ流れと外部空気力学の流れ。流れが低速で移動する大きな空間に入る高速ジェット。ほとんど乱流状態の無い浮力流れ（自然対流）	このモデルは壁関数を使用しません。少なくとも 5 つの壁レイヤを使用します。 k-ε よりも不安定になることがあります。収束には、k-ε よりも多くの反復が必要になります。一般に高速の流れの場合 k-ε と同じ結果が得られます。層流の場合は、層流の選択に類似した結果が得られます。
混合長モデル	いくつかの内部自然対流解析	場合によって、内部浮力駆動の流れに対する実行回数を減らして精度を向上させます。気体の流れ(空気など)のために設計されており、液体の流れに適した結果は生成されません。
渦粘性	より低速の乱流と浮力の流れ。	k-ε モデルほど正確ではなく、数値的にはより安定しています。その他のモデルのいずれかで発散が生じる場合に役立ちます。

SST k- ωに関する追加の注意事項

SST モデルは、Wilcox の k- ω と k-ε のモデルのバリアントを組み合わせたものです。このモデルの利点は次のとおりです。

SST モデルは、他の乱流モデルほど自由流の状態(境界層の外側の流れ)に対する敏感性を示しません。
これらのモデルではせん断応力リミッタが使用されており、よどみ点付近の過度な乱流エネルギーの堆積の回避に役立ちます。
SST モデルでは、SAS や層流と乱流の変化などのその他の拡張機能用のプラットフォームを提供します。
壁の粗さの値が材料定義で事前指定されている場合、SST モデルは壁面の粗さの効果を考慮します。壁の粗さをシミュレートするには、[乱流]ダイアログの[アドバンスト...]ボタンをクリックして、[インテリジェント壁定式化]のチェックマークを外して、インテリジェント壁定式化を無効にします。

自動スタートアップ

自動スタートアップは、自動乱流スタートアップ（ATSU）アルゴリズムをコントロールします。

このアルゴリズムは、乱流流れの解を得るために、多くの計算ステップを使用する。最初にアルゴリズムは渦粘性モデルを使用して10回の収束計算を実行するため、kおよびε方程式は解決されません。この解析結果を初期の予想値として、2方程式乱流モデルを開始します。10回目の収束計算において、kおよびε方程式に対する収束モニターデータの急上昇が現れます。さらにステップを実行し、次第に結果が収束していく。これらのステップを通して、10、20、50回目の収束計算において収束モニターデータに急上昇が現れる可能性があります。50回目の収束計算後、ATSUは自動的にオフになります。

ロックオンを選択すると、ユーザーが手動でオフにしない限り、解析全体を通してATSUがオンになります。50回目の収束計算後に収束が困難な場合（10回の収束計算以内に発散）は、ロックオンを有効にするべきです。ATSUをオンにした場合、乱流解析を確実に収束させるため、少なくとも200回の収束計算を実行するべきである。

拡張を選択すると、ATSUの拡張バージョンが起動します。この方式は、特に圧縮性解析など困難な解析の場合に有用である。このアルゴリズムにおいて実行しなければならない最小収束計算数は400です。

乱流/層流比

乱流/層流比は、層流の値に対する有効（乱流）粘性係数の比です。乱流解析の初期段階において有効粘性を予測するために使用します。ほとんどの乱流解析において、有効粘性係数は層流値より2～3次数大きくなります。一般的に、ほとんどの解析においてデフォルト値が適切である。

混合長モデルの場合、乱流/層流比は渦粘性の上限です。自由流の渦粘性は、この値で最大値に達します。

渦粘性モデルの場合、今すぐリスタートで変更したとしても、これが渦粘性となります。

その他のすべての乱流モデル（k-ε、 RNG、低Re数）の場合、指定された値は渦粘性の開始点または初期値となります。

多くの場合は、大きな空間への、細かく高速なジェット噴射を特徴とする流れの乱流/層流比を1000や10000にまで大きくすると役立ちます。そのような流れは通常、推進力によって生じ、計算の初期段階において大きな渦粘性係数が有効である。

高度なパラメータ

乱流モデルを「微調整」するいくつかのパラメータが追加され、[アドバンスト...]ダイアログで利用することができます。これらのパラメータのほとんどは、乱流流れの「理論の説明」で説明されており、一般的には二方程式乱流理論に精通していない限り、変更するべきではありません。ただし、以下のパラメータは、さらに柔軟に変更することができます。

乱流強度

乱流強度ファクターは、流入口の流れにおける乱流エネルギー量をコントロールします。既定値は 0.05 です。0.5 を超える値を設定することはほとんどありません。流入口における乱流エネルギー量の計算には、次の式を使用します。

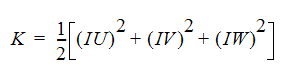
方程式 112

I は強度ファクタ、u、v、w は流速成分です。

インテリジェント壁の定式化

インテリジェント壁定式化は、SST 乱流モデルで安定性と精度を向上させるスケーラブルな壁の定式化です。これは、壁に沿ったメッシュ細分割のレベルに対する結果の感度を緩和します。

インテリジェント壁定式化は、SST k-ω モデルで既定で有効になっています。

さらに、k-ε でもインテリジェント壁式を有効にすることができます。以下のシナリオで有効に機能することが確認されています。

アダプティブメッシュでは、メッシュがリファインされているため、k-ε を用いたインテリジェント壁定式化でパフォーマンス低下は見られません。
k-ε も用いたインテリジェント壁定式化は、サブレイヤ未満(< 35)に下がった Y+ の値に対する感度を削除します。
一部のシミュレーションで k-ε を用いたインテリジェント壁定式化がシミュレーション精度と収束率の改善に効果があることが確認されています。

関連トピック

アドバンスト設定

数学的基盤