해석 특성

• 안정 상태
• 2D 내부 흐름
• 층류
• 비압축성
• 자연 대류

참조

Davis, G. De Vahl 및 Jones, I.P., “Natural convection in a square cavity: a comparison exercise”, Inter. Jour. for Num. Meth. in Fluids, 3, (1983).

문제 설명

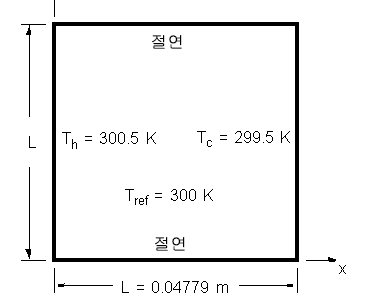
온도 및 속도 분포는 사각형 중공의 층류, 부력 구동에 대해 계산됩니다. 맨 위 및 맨 아래 벽이 단열되고, 왼쪽 및 오른쪽 벽의 고정 온도 차이가 1K입니다.

이 레일리 수는 다음과 같이 계산됩니다.

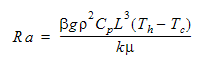
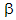• 는 체적 팽창 계수로, 다음과 같이 정의됩니다.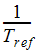

• g는 중력 가속도입니다.

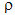• : 밀도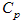

• 는 비열입니다.

• L은 중공 길이입니다.

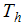• 및 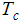는 각각 왼쪽과 오른쪽 벽의 온도입니다.

• k는 유체 전도율입니다.

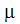• 는 점도입니다.

• 여기서 레일리 수는 10,000입니다.

이 문제를 분석하여 Autodesk® CFD의 유체 흐름 및 열 전달 모델링 기능을 확인합니다. 정확도는 중공에서 특정 위치에 있는 속도 구성요소를 비교하여 평가합니다. 속도 및 좌표는 Davies, et al. (1983)에 따라 다음과 같이 정규화됩니다.

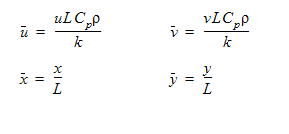
형상 및 경계 조건

결과

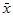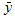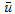, , 및 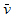에 대해 위에 정의된 표현식을 사용하면 다음 결과가 계산됩니다.

	벤치마크	2018: 빌드 20170308	오류 비율	2019: 빌드 20180130	오류 비율
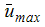	16.178	16.191	0.079	16.185	0.04399
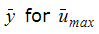	0.823	.825	.243	.825	.243
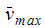	19.617	19.666	.251	19.651	.175
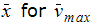	0.119	.120	.840	.120	.840