通用计算公式
弹簧外径
D 1 = D + d [in]
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
弹簧内径
D 2 = D - d [in]
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
工作变形量
H = L 8 - L 1 = s 8 - s 1 [in]
其中:
|
L 8 |
满载时的弹簧长度 [in] |
|
|
L 1 |
预承载时的弹簧长度 [in] |
|
|
s 8 |
满载时的弹簧变形量 [in] |
|
|
s 1 |
预承载时的弹簧变形量 [in] |
簧眼的高度
![]()
其中:
|
L 0 |
自由弹簧的长度 [in] |
|
|
L Z |
弹簧螺旋部分的长度 [in] |
弹簧指数
c = D/d [-]
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
Wahl 修正系数
![]()
其中:
|
c |
弹簧指数 [-] |
初始拉力
![]()
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
|
|
τ 0 |
自由状态应力 [psi] |
|
|
K w |
曲度系数 [-] |
弹簧产生的一般作用力
![]()
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
|
| τ |
扭应力是每个单位区域的力。通常情况下是弹簧材料的扭应力 [psi] |
|
|
K w |
曲度系数 [-] |
|
|
G |
弹簧材料的弹性模量 [psi] |
|
|
s |
通常的弹簧变形量 [in] |
|
|
n |
有效簧圈数 [-] |
|
|
F 0 |
弹簧初始拉力 [lb] |
弹簧钢度
![]()
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
|
|
G |
弹簧材料的弹性模量 [psi] |
|
|
s |
通常的弹簧变形量 [in] |
|
|
n |
有效簧圈数 [-] |
|
|
F 8 |
满载时弹簧的工作扭矩 [psi] |
|
|
F 1 |
最小承载时弹簧的工作扭矩 [psi] |
|
|
H |
工作变形量 [in] |
弹簧设计计算
在弹簧设计过程中,根据特定载荷、材料和装配尺寸设置钢丝直径、簧圈数和弹簧自由长度 L 0 。
![]()
根据上述公式,如果计算出的弹簧与 τ 0 应力的所有钢丝直径均不匹配,则将在建议范围内使用自由状态下更正的应力值重新计算。
![]()
没有初始拉力的弹簧是针对建议的平均节距值 t = 0.35 D [in] 设计的。
如果计算的弹簧与选定节距的所有钢丝直径都不匹配,则使用建议的 D ≤ t ≤ 0.4 D [in] 范围内的修正节距值重新计算弹簧。
基于某些弹簧几何尺寸的 τ 8 ≤ u s τ A 强度条件和建议范围(L 0 ≤ D 和 L 0 ≤ 31.5 in 和 4 ≤ D/d ≤ 16 和 n ≥ 2)进行弹簧设计。
指定的载荷、材料和弹簧装配尺寸
首先,校核用于计算的输入值并对其进行计算。
接下来,计算自由状态下的弹簧长度。
![]()
完成计算后,设计钢丝直径、簧圈数和弹簧直径,以使弹簧钩高度符合选定的钩类型,并满足强度和几何条件。弹簧设计必须符合规范中所限制的任何弹簧直径值。
在设计过程中,按照从小到大的顺序,计算符合强度和几何条件的所有弹簧钢丝直径。测试弹簧钩环高度和圈数。如果所有条件均满足,则将使用选定的值完成设计,而不考虑其他符合的弹簧钢丝直径。
计算出的弹簧钩高度必须在 d ≤ o ≤ 30 d 范围内。钢丝直径、圈数和弹簧直径的组合必须最终使计算出的弹簧钩环高度与基本钩环类型的高度相符。基本钩类型的选择步骤如下:首先考虑满圈,然后考虑内部满圈,接着再考虑其他钩类型。
指定的载荷、材料和弹簧直径
首先,校核用于计算的输入值。
完成校核后,设计钢丝直径、簧圈数、弹簧自由长度和装配尺寸,以使弹簧钩高度符合选定的钩类型。此外,还必须满足上述强度和几何条件。如果规范中规定了装配尺寸 L 1 或 L 8 ,或者限制了工作弹簧变形值,那么弹簧设计必须符合该条件。否则,装配尺寸和自由弹簧长度的限制将由指定的弹簧直径和最小或最大许用钢丝直径的几何条件确定。
使用指定钢丝直径设计弹簧的公式。

其中,τ 8 = 0.85 τ A 值用于计算弹簧满载状态下弹簧材料的扭应力值。
如果无法为此钢丝直径设计合适的弹簧尺寸组合,将继续对所有适合的钢丝直径进行几何考察。按照从小到大的顺序测试弹簧钢丝直径,直到找到的弹簧钩环高度符合上述条件的圈数。使用选定的值完成设计,而不考虑其他适合的钢丝直径,并且以最小的弹簧钢丝直径和最少的圈数设计弹簧。
计算出的弹簧钩高度必须在 d ≤ o ≤ 30 d 范围内。根据由此方法计算的钩环高度选择相应的钩环类型。钢丝直径、圈数、弹簧自由长度和装配尺寸的组合必须最终使计算出的弹簧钩环高度与基本钩环类型的高度相符。基本钩类型的选择步骤如下:首先考虑满圈,然后考虑内部满圈,接着再考虑其他钩类型。
指定的最大作用力、确定的材料、装配尺寸及弹簧直径
首先,校核用于计算的输入值并对其进行计算。
然后,设计钢丝直径、簧圈数、弹簧自由长度和 F 1 最小作用力,以使弹簧钩高度符合选定的钩类型。此外,还必须满足上述强度和几何条件。
使用指定钢丝直径设计弹簧的公式。

其中,τ 8 = 0.9 τ A 值用于计算弹簧满载状态下弹簧材料的扭应力值。
如果无法为此钢丝直径设计合适的弹簧尺寸组合,将继续对所有适合的钢丝直径进行几何考察。按照从小到大的顺序测试弹簧钢丝直径,直到找到的弹簧钩环高度符合上述条件的圈数。使用选定的值完成设计,而不考虑其他适合的钢丝直径,并且以最小的弹簧钢丝直径和最少的圈数设计弹簧。
弹簧校验计算
计算装配尺寸的相应值以及指定载荷、材料及弹簧尺寸的工作弹簧变形。
首先,校核用于计算的输入值。然后,使用以下公式计算装配尺寸。
预载时的弹簧长度
![]()
满载时的弹簧长度
![]()
其中:
|
F 1 |
最小承载时弹簧的工作扭矩 [psi] |
|
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
|
|
G |
弹簧材料的弹性模量 [psi] |
|
|
L 0 |
自由弹簧的长度 [in] |
|
|
n |
有效簧圈数 [-] |
|
|
F 8 |
满载时弹簧的工作扭矩 [psi] |
工作变形量
H = L 1 - L 8 [in]
作用力计算
针对指定材料、装配尺寸和弹簧尺寸,计算弹簧在其工作状态下产生的工作扭矩。首先,校核并计算输入数据,然后使用以下公式计算工作扭矩。
最小作用力
![]()
最大作用力
![]()
弹簧输出参数计算
可用于所有类型的弹簧计算,计算时按照以下顺序进行。
弹簧钩高度系数
![]()
弹簧钢度
![]()
螺旋部分的长度
|
没有初始拉力的弹簧 |
|
|
L z = t n + d [in] |
|
|
具有初始拉力的弹簧 |
|
|
L z = 1.03 (n + 1) d [in] |
|
预载时的弹簧变形量
s 1 = L 1 - L 0 [in]
总弹簧变形量
s 8 = L 8 - L 0 [in]
预载状态下弹簧材料的扭应力
![]()
满载状态下弹簧材料的扭应力
![]()
弹簧极限力
![]()
极限状态下的变形量
![]()
其中:
|
k |
弹簧钢度 [lb/in] |
|
|
F 9 |
承受极限载荷的弹簧工作扭矩 [lb] |
|
|
F 0 |
弹簧初始拉力 [lb] |
弹簧极限长度
L 9 = L 0 + s 9 [in]
弹簧变形能
![]()
展开的钢丝长度
|
l = 3.2 D n + l 0 [in] |
|||
|
其中,设计的钩长度为 l 0 : |
|||
|
对于半钩 |
|||
|
l 0 = π D + 4 o - 2 D - 2 d [in] |
|||
|
对于满圈 |
|||
|
l 0 = 2 (π D - 2 d) [in] |
|||
|
对于端面满圈 |
|||
|
l 0 = 2 (π D - 2 d) [in] |
|||
|
对于内部满圈 |
|||
|
l 0 = 2 (π D - d) [in] |
|||
|
对于提升弹簧钩 |
|||
|
l 0 = π D + 2 o - D + 3 d [in] |
|||
|
对于双股满圈 |
|||
|
l 0 = 4 π D [in] |
|||
|
对于端面双股满圈 |
|||
|
l 0 = 4 π D [in] |
|||
|
对于非指定的钩类型 |
|||
|
l 0 = 0 [in] |
|||
弹簧质量
![]()
弹簧自振频率
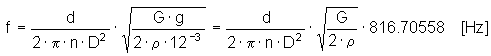
弹簧载荷的校核
τ 8 ≤ u s τ A
所用变量概述:
|
d |
钢丝直径 [in] |
|
k |
弹簧钢度 [lb/in] |
|
D |
弹簧中径 [in] |
|
D 1 |
弹簧外径 [in] |
|
D 2 |
弹簧内径 [in] |
|
F |
弹簧产生的一般作用力 [lb] |
|
G |
弹簧材料的弹性切变模量 [psi] |
|
H |
工作变形量 [in] |
|
c |
弹簧指数 [-] |
|
K w |
曲度系数 [-] |
|
l |
弹簧展开长度 [in] |
|
L |
通常情况下的弹簧长度 [in] |
|
L Z |
弹簧螺旋部分的长度 [in] |
|
m |
弹簧质量 [lb] |
|
n |
有效簧圈数 [-] |
|
o |
弹簧钩环高度 [in] |
|
t |
自由状态有效螺旋之间的节距 [in] |
|
s |
通常的弹簧变形量(伸张度)[in] |
|
u s |
|
| ρ |
弹簧材料的密度 [lb/ft3] |
| τ |
扭应力是每个单位区域的力。通常情况下是弹簧材料的扭应力 [psi] |
|
τ A |
弹簧材料的许用扭应力 [psi] |