采用公制单位或英制单位进行计算。采用 ANSI 标准集时,计算中采用的是英制单位。
在 XY 和 XZ 平面中进行计算,并且计算这两个平面的平方和。
计算的参数
无载荷时弹簧的截锥的自由高度
h = H - t [mm, in]
其中:
|
H |
无载荷时弹簧的高度 [mm, in] |
|
|
t |
弹簧碟簧厚度 [mm, in] |
直径比
![]()
其中:
|
D |
弹簧外径 [mm, in] |
|
|
d |
弹簧内径 [mm, in] |
计算系数 α
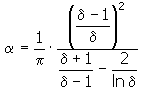
计算系数 β
![]()
计算系数 γ
![]()
弹簧片的最大允许变形量
s m = h [mm, in]
其中:
|
h |
无载荷时弹簧的截锥的自由高度 [mm, in] |
弹簧最大变形(极限变形)时的受力
![]()
其中:
|
E |
弹簧的弹性模量 [MPa, psi] |
|
|
t |
弹簧碟簧厚度 [mm, in] |
|
|
s m |
最大弹簧变形量 [mm, in] |
|
| μ |
泊松比 [-] |
|
| α |
计算系数 [-] |
|
|
D |
弹簧外径 [mm, in] |
弹簧在变形量为 s 时施加的力

其中:
|
E |
弹簧的弹性模量 [MPa, psi] |
|
|
t |
弹簧碟簧厚度 [mm, in] |
|
|
s |
单片弹簧的工作变形量 [mm, in] |
|
| μ |
泊松比 [-] |
|
| α |
计算系数 [-] |
|
|
D |
弹簧外径 [mm, in] |
|
|
h |
无载荷时弹簧的截锥的自由高度 [mm, in] |
弹簧在变形量为 s 时的最大压应力
![]()
其中:
|
E |
弹簧的弹性模量 [MPa, psi] |
|
|
t |
弹簧碟簧厚度 [mm, in] |
|
|
s |
单片弹簧的工作变形量 [mm, in] |
|
| μ |
泊松比 [-] |
|
| α |
计算系数 [-] |
|
|
D |
弹簧外径 [mm, in] |
|
|
h |
无载荷时弹簧的截锥的自由高度 [mm, in] |
|
| γ |
计算系数 [-] |
组合弹簧的总弹簧片数
χ = n i [-]
其中:
|
n |
叠合组合中的弹簧叠合层数 [-] |
|
|
i |
对合组合中的弹簧对合片数或者复合组合中叠合组合的弹簧数 [-] |
组合弹簧的工作行程(变形量)
z = i s [mm, in]
其中:
|
i |
对合组合中的弹簧对合片数或者复合组合中叠合组合的弹簧数 [-] |
|
|
s |
单片弹簧的工作变形量 [mm, in] |
组合弹簧施加的力
F = n F 1 [N, lb]
其中:
|
n |
叠合组合中的弹簧叠合层数 [-] |
|
|
F 1 |
单片弹簧的载荷 [N, lb] |
空载状态下组合弹簧的长度
L 0 = i (h + n t ) [mm, in]
其中:
|
h |
无载荷时弹簧的截锥的自由高度 [mm, in] |
|
|
i |
对合组合中的弹簧对合片数或者复合组合中叠合组合的弹簧数 [-] |
|
|
n |
叠合组合中的弹簧叠合层数 [-] |
|
|
t |
弹簧碟簧厚度 [mm, in] |
负载状态下组合弹簧的长度
L = L 0 - z [mm, in]
其中:
|
L 0 |
无载荷状态下组合弹簧的自由长度 [mm, in] |
|
|
z |
组合弹簧的工作行程(变形量)[mm, in] |
使用的所有变量综述:
|
d |
弹簧内径 [mm, in] |
|
D |
弹簧外径 [mm, in] |
|
F 1 |
单片弹簧的载荷 [N, lb] |
|
E |
弹簧的弹性模量 [MPa, psi] |
|
t |
弹簧碟簧厚度 [mm, in] |
|
s |
单片弹簧的工作变形量 [mm, in] |
| μ |
泊松比 [-] |
|
i |
对合组合中的弹簧对合片数或者复合组合中叠合组合的弹簧数 [-] |
|
n |
叠合组合中的弹簧叠合层数 [-] |
|
H |
无载荷时弹簧的高度 [mm, in] |