轴承因摩擦而生热。产生的热与通过轴承传导的热应保持平衡。通过轴承外壳和连接轴,热从轴承传导到周围环境中。热传导是通过传导和辐射实现的,并且主要传给流动的润滑剂。
产生的热量的主要部分(估计超过 75%)通过润滑剂从轴承传导出来。因此润滑剂的温度会从入口的低温度流经轴承,上升到出口处的高温度。轴承热平衡计算的目的就是获得轴承出口处的平均润滑剂温度,此处选定的润滑剂将摩擦产生的热能与通过轴承传导的热量保持平衡。
轴承通过润滑剂传导的热量的多少取决于润滑剂的密度和粘度。因为润滑剂的密度和粘度都会随着温度的改变而改变,所以需要使用逐次逼近法来获得出口处润滑剂的温度。用户所预期的出口处润滑剂温度作为该计算逼近算法的基础。当设计温度和计算温度的差低于 2 摄氏度时,即结束计算。如果温差大于 2 摄氏度,则不能忽视,因为这会导致油层油粘度和载荷能力发生显著变化。
以下内容说明了所有用于轴承热平衡的计算表达式:
动压导致的油溢出
如果轴承没有进行边缘紧固,油就会由于动压而通过边缘润滑缝隙漏出。漏油量为:
V z = 0.125 R * 1 ε d 3 φω 10 -3 [cm 3 s -1 ]
其中,R * 1 溢出特征数通过各个轴承相对宽度、相对轴颈偏心和润滑剂入口角度示意图来确定。
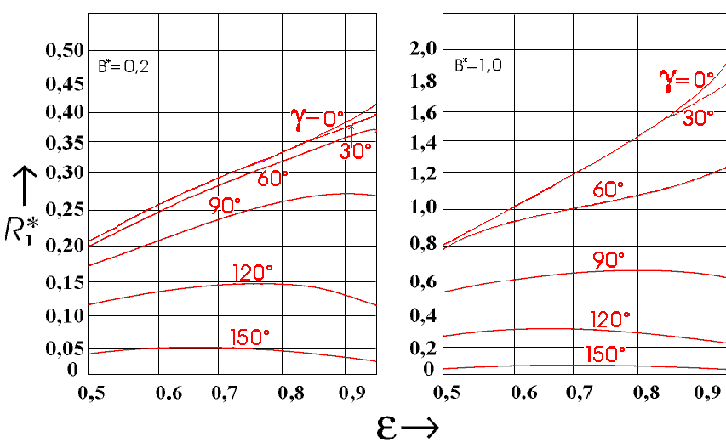
入口压力导致的油溢出
如果油是通过入口压力供应给轴承的,那么油溢出量会根据各自的值而增加。使用以下表达式确定通过径向(即圆周)槽润滑的轴承中因入口压力而流失的油量:
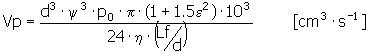
通过润滑孔或轴向润滑槽润滑的轴承:
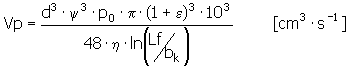
循环的油量
原先在真空层的部分油会返回到压力层并不断循环。其数量为
V z = 0.125 R * 2 ε d 3 φω 10 -3 [cm 3 s -1 ]
取决于 R * 2 特征再循环数,可根据轴承相对宽度和相对轴颈偏心在示意图中找到该值:
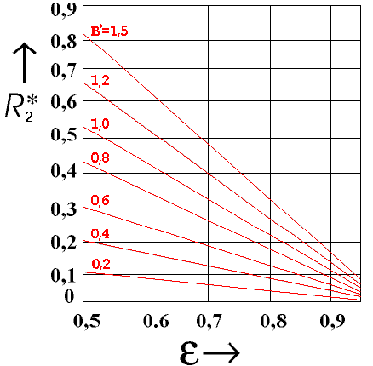
供应给轴承的润滑剂总量
润滑剂总量根据以下条件来决定:
- 没有压力但有再循环情况下的润滑剂供应。只增加了由于溢出而造成的损失。
V = V z [cm 3 s -1 ]
- 没有压力且没有再循环情况下的润滑剂供应。通过润滑层传递的油因冷却而被清除或冲走。
V = V z + V u [cm 3 s -1 ]
- 再循环情况下的压力油入口。
V = V z + V p [cm 3 s -1 ]
- 清除或冲走变热的油的压力油入口。
V = V z + V p + u [cm 3 s -1 ]
填充槽的真空部分
润滑层的压力部分中连续的薄油层开始分解,同时轴承槽开始填充从油释放的气体和从轴承边缘吸收的气体,并且填充油汽。薄油层在真空部分中蒸发得越多,摩擦损失也就会降低得越多。未承载的套筒部分的减轻或去除会导致薄油层的分解。相反,如果满足以下两个条件,润滑槽就会被完全填充:
p o > 0.4 [MPa]
![]()
在这些条件中摩擦损失为最高。
摩擦系数
对于润滑槽的部分填充:
μ = φΜ * 1 [-]
对于润滑槽的完全填充:
μ = φΜ * 2 [-]
其中,M * 1 、M * 2 特征摩擦数通过相对轴承宽度和相对轴颈偏心示意图来确定:
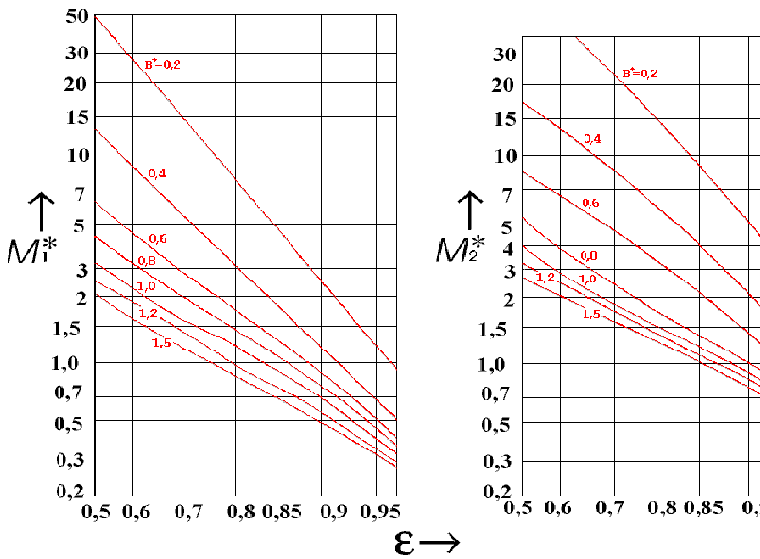
轴承中由于摩擦导致的能量损失
![]()
传递给周围环境的摩擦功率为
P U = 3.5 π d L α W (T V - T U ) 10 -6 [W]
其中散热系数为
α W = 12 + 8 ν V / 1.2 [W m -2 K -1 ] for ν V ≤ 1.2 m s -1
![]()
for ν V ≤ 1.2 m s -1
轴承出口处在平均润滑剂温度时的润滑剂的具体热容量为
c T = 4.588 T V - 5.024.10 -3 ρ 2 20 + 7.1156 ρ 20 - 619.646 [J kg -1 K -1 ]
轴承出口处在平均润滑剂温度时的润滑剂密度为
ρ T = ρ 20 - 0.65 (T - 20) [kg m -3 ]
在入口和出口间的润滑剂预热为
![]()
其中内部冷却系数表示了从轴承传导的相对热量,其值为:
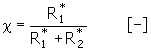
轴承出口处润滑剂温度计算的平均值为
T v = T o + ΔT [°C]
所用变量的含义:
|
b k |
润滑孔径或轴向润滑槽长度 [mm]。 |
|
d |
轴颈直径 [mm]。 |
|
Δd |
径向间隙 [mm]。 |
|
F |
载荷力 [N]。 |
|
L |
轴承宽度 [mm]。 |
|
L f |
主动轴承宽度 [mm]。 |
|
p 0 |
润滑剂入口压力 [MPa]。 |
|
T U |
轴承周围环境的温度 [°C]。 |
|
T V |
轴承出口处的润滑剂平均温度 [°C]。 |
|
T 0 |
润滑剂入口温度 [°C]。 |
|
v H |
轴承轴颈的圆周速度 [m s -1 ]。 |
|
v V |
气流速度 [m s -1 ]。 |
|
α W |
散热系数 [W m -2 K -1 ]. |
| ε |
相对轴颈偏心 [-]。 |
| η |
轴承出口处平均温度时的润滑剂动态粘度 [Pa s]。 |
|
ρ 20 |
温度为 20°C 时的润滑剂密度 [Kg m -3 ]。 |
| χ |
内部冷却系数 [-]。 |
| φ |
相对径向间隙 [mm]。 |
| ω |
轴承轴颈动压作用的角速度 [s -1 ]。 |