Vzorce pro výpočty tolerance

Tip: Chcete-li provádět výpočty jednorozměrné analýzy tolerance, zvažte použití doplňku Autodesk® Inventor® Tolerance Analysis. Aplikace Inventor Tolerance Analysis nabízí bohatou sadu nástrojů, které vám umožní lépe porozumět dopadu mechanického upevnění a výkonu na základě souhrnné rozměrové odchylky.

Další informace naleznete v části Definování řetězců tolerance.

Základní vztahy pro lineární uzavřené obvody kót, které jsou použité v aplikaci lze odvodit z následujícího obrázku:

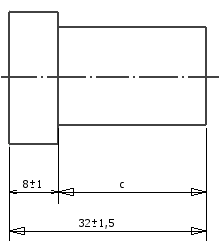
a = 32 ± 1,5 mm, b = 8 ± 1 mm

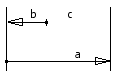
Zvětšující a zmenšující členy

Roste-li zvětšující člen, zvětšuje se uzavírající člen (při konstantních dalších členech). Roste-li zmenšující člen, zmenšuje se uzavírající člen (při konstantních dalších členech).

Uzavírající člen:	1. c = a - b
Horní mezní rozměr uzavírajícího členu:	2. c max = a max - b min
Dolní mezní rozměr uzavírajícího členu:	3. c min = a min - b max
Tolerance uzavírajícího členu (odečtením 3. od 2.)	4. c max - c min = a max - a min - (b min - b max )
Například	5. T c = T a + T b

Poznámka: Tolerance uzavírajícího členu se rovná součtu tolerancí ostatních členů uzavřeného obvodu kót

Obecně lineární obvody vyhovují následujícím rovnicím.

Podobně lze zobecnit pro lineární obvody i rovnice 2. a 3.

Horní mezní rozměr uzavírajícího členu se rovná rozdílu součtu horních mezních rozměrů zvětšujících členů a součtu dolních mezních rozměrů zmenšujících členů.

Dolní mezní rozměr uzavírajícího členu se rovná rozdílu součtu dolních mezních rozměrů zvětšujících členů a součtu horních mezních rozměrů zmenšujících členů.

Jmenovitý rozměr uzavírajícího členu se podle rovnice 1. obecně vyjádří:

Horní mezní úchylka uzavírajícího členu.

Dolní mezní úchylka uzavírajícího členu.