Výpočetní vzorce pro tlačné pružiny v metrických jednotkách

Obecné výpočtové vzorce

Součinitel využití materiálu

Součinitel bezpečnosti při mezi únavy

Vnější průměr pružiny

D ₁ = D + d [mm]

kde:

	D	střední průměr pružiny [mm]
	d	průměr drátu [mm]

Vnitřní průměr pružiny

D ₂ = D - d [mm]

kde:

	D	střední průměr pružiny [mm]
	d	průměr drátu [mm]

Pracovní vychýlení

H = L ₁ - L ₈ = s ₈ - s ₁ [mm]

kde:

	L 8	délka plně zatížené pružiny [mm]
	L 1	délka předpružené pružiny [mm]
	s 8	deformace plně zatížené pružiny [mm]
	s 1	deformace předpružené pružiny [mm]

Index pružiny

c = D/d [-]

kde:

	D	střední průměr pružiny [mm]
	d	průměr drátu [mm]

Wahlův korekční součinitel

kde:

	c	poměr vinutí [-]
	d	průměr drátu [mm]

Celková síla vyvinutá pružinou

kde:

	d	průměr drátu [mm]
	τ	napětí materiálu pružiny v ohybu obecně [MPa]
	D	střední průměr pružiny [mm]
	K w	korekční součinitel Wahl [-]
	G	modul pružnosti materiálu pružiny [MPa]
	s	deformace (natažení) pružiny obecně [mm]
	n	počet činných závitů [-]
	F 0	předpětí pružiny [N]

Konstanta pružiny

kde:

	d	průměr drátu [mm]
	F 8	pracovní síla plně zatížené pružiny [MPa]
	D	střední průměr pružiny [mm]
	H	pracovní zdvih [mm]
	G	modul pružnosti materiálu pružiny [MPa]
	n	počet činných závitů [-]
	F 1	pracovní síla minimálně zatížené pružiny [MPa]

Střední průměr pružiny

kde:

	d	průměr drátu [mm]
	k	tuhost pružiny [N/in]
	G	modul pružnosti materiálu pružiny [MPa]
	n	počet činných závitů [-]

Vychýlení pružiny obecně

s = F / k [mm]

kde:

	F	Pracovní síla vyvinutá pružinou obecně [N]
	k	tuhost pružiny [N/in]

Délka volné pružiny

L ₀ = L ₁ + s ₁ = L ₈ + s ₈ [mm]

kde:

	L 8	délka plně zatížené pružiny [mm]
	L 1	délka předpružené pružiny [mm]
	s 8	deformace plně zatížené pružiny [mm]
	s 1	deformace předpružené pružiny [mm]

Výpočet návrhu pružiny

V návrhu pružiny je pro měrné zatížení, materiál a montážní rozměry nebo průměr pružiny navržen průměr drátu, počet závitů a délka pružiny ve volném stavu L0. U pružin s doporučenými průměry drátu by měla být rozteč mezi závity pružiny ve volném stavu v intervalu 0,3 D ≤ t ≤ 0,6 D [mm].

Návrh pružiny je založen na pevnostní podmínce τ ₈ ≤u _s τ _A a na doporučených rozmezích některých geometrických rozměrů pružiny:

L ₈ ≥ L _minF a D ≤ L ₀ ≤ 10 D a L ₀ ≤ 31,5 palce a 4 ≤ D/d ≤ 16 a n≥ 2 a 12 d ≤ t < D

kde:

	D	střední průměr pružiny [mm]
	d	průměr drátu [mm]
	rozteč činných závitů ve volném stavu	rozteč činných závitů ve volném stavu [mm]
	τ 8	napětí materiálu plně zatížené pružiny v krutu [MPa]
	τ A	dovolené napětí materiálu pružiny v krutu [MPa]
	u s	součinitel využití materiálu [-]
	L 8	délka plně zatížené pružiny [mm]
	L minF	mezní zkušební délka pružiny [mm]
	n	počet činných závitů [-]

Pokud jsou v zadání uvedeny podmínky bezpečnosti při vzpěru a podmínky kontroly na únavové namáhání, musí jim pružina vyhovovat.

Postupy návrhu pružiny pro různé typy návrhu jsou uvedeny dále.

Postupy navrhování

1. Dané zatížení, materiál a kóty sestavy pružiny

Nejprve zkontrolujte a vypočtěte vstupní hodnoty.

Navrhněte průměr drátu a počet závitů v souladu s požadavky na pevnost a geometrické vlastnosti uvedenými v předchozí tabulce. Nebo použijte hodnoty průměru v technických údajích.

Během návrhu program počítá postupně od nejmenšího po největší všechny průměry drátu pružiny, které odpovídají pevnostním a geometrickým podmínkám. Jestliže jsou splněny všechny podmínky, dokončí se návrh s vybranými hodnotami bez ohledu na ostatní odpovídající průměry drátu pružiny. To znamená, že se program snaží navrhnout pružinu s minimálním průměrem drátu a minimálním počtem závitů.

2. Návrh pružiny pro dané zatížení, materiál a průměr pružiny

Nejprve zkontrolujte vstupní hodnoty pro výpočet.

Navrhujte průměr drátu, počet vinutí, volnou délku pružiny a kóty sestavy v souladu s pevnostními a geometrickými podmínkami uvedenými výše, nebo v souladu s jakýmikoliv kótami sestavy L ₁ nebo L ₈ uvedenými ve specifikaci, nebo dle jakékoliv hodnoty pracovního vychýlení pružiny, které je omezeno.

Při návrhu pružiny s daným průměrem drátu použijte následující vzorec.

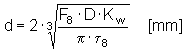
kde:

	τ 8 = 0,85 τ A
	F 8	pracovní síla plně zatížené pružiny [MPa]
	D	střední průměr pružiny [mm]
	K w	korekční součinitel Wahl [-]
	τ 8	napětí materiálu plně zatížené pružiny v krutu [MPa]
	τ A	dovolené napětí materiálu pružiny v krutu [MPa]

Pokud nelze pro tento průměr drátu navrhnout žádnou vhodnou kombinaci rozměrů pružiny, testují se všechny průměry drátu pružiny, které vyhovují pevnostním a geometrickým podmínkám (od nejmenšího po největší). Testují se vhodné počty závitů, zda návrh pružiny vyhovuje daným podmínkám. V tomto případě se návrh ukončí s vybranými hodnotami bez ohledu na ostatní vhodné průměry drátu pružiny a pružina se navrhne s nejmenším průměrem drátu a nejmenším počtem závitů.

3. Návrh pružiny pro danou maximální pracovní sílu, známý materiál, kóty sestavy a průměr pružiny

Nejprve zkontrolujte vstupní hodnoty pro výpočet.

Poté je průměr drátu, počet závitů, volná délka pružiny a minimální pracovní síla F ₁ navržen tak, aby byly splněny výše uvedené pevností a geometrické podmínky.

Přednostně se program snaží navrhnout pružinu pro průměr drátu vycházející ze vzorce:

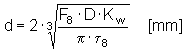
kde:

	τ 8 = 0,85 τ A
	F 8	pracovní síla plně zatížené pružiny [MPa]
	D	střední průměr pružiny [mm]
	K w	korekční součinitel Wahl [-]
	τ 8	napětí materiálu plně zatížené pružiny v krutu [MPa]
	τ A	dovolené napětí materiálu pružiny v krutu [MPa]

Pokud nelze pro tento průměr drátu navrhnout žádnou vhodnou kombinaci rozměrů pružiny, testují se všechny průměry drátu pružiny, které vyhovují pevnostním a geometrickým podmínkám (od nejmenšího po největší). Ověřuje vhodné počty závitů, zda navržená pružina splňuje všechny požadované podmínky. V takovém případě je návrh ukončen se zvolenými hodnotami, bez ohledu na další vyhovující průměry drátu pružiny. To znamená, že se program snaží navrhnout pružinu s minimálním průměrem drátu a minimálním počtem závitů.

Kontrolní výpočet pružiny

Vypočítá odpovídající hodnoty montážních rozměrů a pracovní zdvih pro dané zatížení, materiál a rozměry pružiny.

Nejprve se zkontrolují vstupní hodnoty pro výpočet. Podle následujících vztahů jsou spočítány montážní rozměry.

Délka pružiny s předpětím

Délka plně zatížené pružiny

kde:

	L 0	délka volné pružiny [mm]
	F 1	pracovní síla minimálně zatížené pružiny [mm]
	n	počet činných závitů [-]
	D	střední průměr pružiny [mm]
	G	modul pružnosti materiálu pružiny [MPa]
	d	průměr drátu [mm]
	F 8	pracovní síla plně zatížené pružiny [MPa]

Pracovní vychýlení

H = L ₁ - L ₈ [mm]

Výpočet pracovních sil

V tomto výpočtu se pro určený materiál, montážní rozměry a rozměry pružiny vypočítají odpovídající síly vyvinuté pružinou v jejích pracovních stavech. Nejprve se zkontrolují a vypočítají vstupní data, potom se podle následujících vzorců vypočítají pracovní síly:

Minimální pracovní síla

Maximální pracovní síla

Výpočet výstupních parametrů pružiny

Tato část je společná pro všechny typy výpočtu pružiny a provádí se v následujícím pořadí.

Konstanta pružiny

Teoretická mezní délka pružiny

L ₉ = (n + n _z + 1 - z ₀ ) d [mm]

Mezní zkušební délka pružiny

L _minF = L _9max + S _amin [mm]

kde horní mezní délka pružiny v mezním stavu L _9max :

pro neobrobené dosedací plochy
	L 9max = 1,03 L 9 [mm]
pro obrobené dosedací plochy a (n + nz) <= 10,5
	L 9max = (n + n z ) d [mm]
pro obrobené dosedací plochy a (n + nz) > 10,5
	L 9max = 1,05 L 9 [mm]

Součet nejmenších přípustných vůlí mezi činnými závity ve stavu plného zatížení,

přičemž pro hodnoty poměru vinutí c < 5 je použita hodnota c = 5.

Vychýlení pružiny v mezním stavu

s ₉ = L ₀ - L ₉ [mm]

Mezní síla pružiny

F ₉ = k S ⁹ [N]

Prostor mezi závity

Rozteč činných závitů

t = a + d [mm]

Vychýlení předpružené pružiny

s ₁ = L ₀ - L ₁ [mm]

Celkové vychýlení pružiny

s ₈ = L ₀ - L ₈ [mm]

Napětí materiálu pružiny v krutu v předpruženém stavu

Napětí materiálu pružiny v krutu v plně zatíženém stavu

Dosedací napětí

Rozvinutá délka drátu

l = 3.2 D (n + n _z ) [mm]

Hmotnost pružiny

Deformační energie pružiny

Přirozený kmitočet rázů v pružině

Kritická (mezní) rychlost pružiny z hlediska vzniku vzájemných nárazů závitů vlivem setrvačnosti

Kontrola zatížení pružiny

τ ₈ ≤u _s τ _A a L _minF ≤ L ₈

Význam použitých proměnných:

a	vůle mezi činnými závity ve volném stavu [mm]
k	tuhost pružiny [N/mm]
d	průměr drátu [mm]
D	střední průměr pružiny [mm]
D 1	vnější průměr pružiny [mm]
D 2	vnitřní průměr pružiny [mm]
F	pracovní síla vyvinutá pružinou obecně [N]
G	modul pružnosti materiálu pružiny [MPa]
c	poměr vinutí [-]
H	pracovní zdvih [mm]
K w	korekční součinitel Wahl [-]
k f	součinitel bezpečnosti na mezi únavy [-]
l	rozvinutá délka drátu [mm]
L	délka pružiny obecně [mm]
L 9max	horní mez délky pružiny v mezním stavu [mm]
L minF	mezní zkušební délka pružiny [mm]
m	hmotnost pružiny [kg]
N	životnost pružiny při střídavém namáhání v tisících cyklů [-]
n	počet činných závitů [-]
n z	počet závěrných závitů [mm]
t	rozteč činných závitů ve volném stavu [mm]
s	deformace (natažení) pružiny obecně [mm]
s amin	součet nejméně dovoleného prostoru mezi činnými závity pružiny [mm]
u s	součinitel využití materiálu [-]
z 0	počet nečinných závitů [-]
ρ	hustota materiálu pružiny [kg/m 3 ]
σ ult	mez pevnosti materiálu pružiny v tahu [MPa]
τ	napětí materiálu pružiny v ohybu obecně [MPa]
τ e	mez únavy materiálu cyklicky zatěžované pružiny v krutu [MPa]
τ A8	dovolené napětí materiálu pružiny v krutu [MPa]