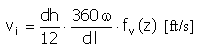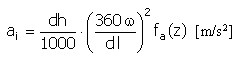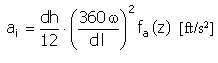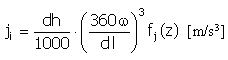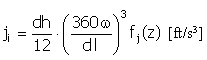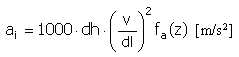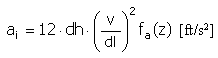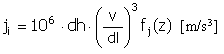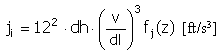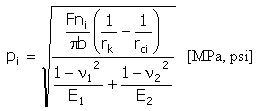Vstupní údaje:
- základní poloměr r 0 (rotační a válcové vačky),
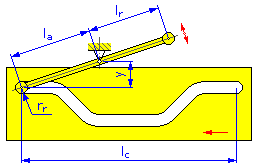
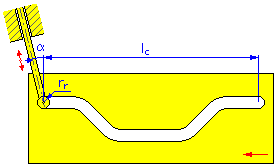
- délka pohybu l c (posuvné vačky),
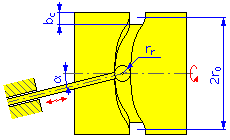
- šířka vačky b c ,
- poloměr kladky r r ,
- šířka kladky b r (válcového tvar zdvihátka),
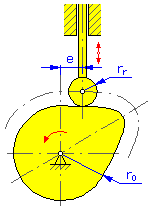
- excentricita e (rotační vačky pro posuvné zdvihátko),
- úhel excentricity α (posuvné a válcové vačky pro posuvné zdvihátko),
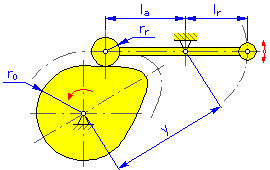
- vzdálenost čepu y (rotační a posuvné vačky pro otočné rameno),
- délka ramene l a (rotační a posuvné vačky pro otočné rameno),
- reakční rameno l r (rotační a posuvné vačky pro otočné rameno),
- rychlost ω (rotační a válcové vačky),
- rychlost v (posuvné vačky),
- síla na zdvihátku F,
- zrychlená tíha m,
- tuhost pružiny c,
- dovolený tlak p A1 ,
- modul pružnosti materiálu vačky E 1 ,
- Poissonova konstanta materiálu vačky μ 1 ,
- dovolený tlak p A2 ,
- modul pružnosti materiálu kladičky E 2 ,
- Poissonova konstanta materiálu kladičky μ 2 .
|
Rotační vačka |
|
|
|
|
|
Posuvná vačka |
|
|
|
|
|
Válcová vačka |
|
 |
|
|
Vnější průměr = 2r 0 + b c |
|
|
Vnitřní průměr = 2r 0 + b c |
|
Segmenty vačky
- zdvihová funkce f y (z) [ul],
- poměr první části k r (jen pro parabolický pohyb a pohyb parabolický s lineární částí),
- lineární část k l (jen pro pohyb parabolický s lineární částí),
- počáteční pozice pohybu L 0 [°; mm, in],
- konečná pozice pohybu L [°; mm, in],
- délka pohybu segmentu dL = L - L 0 [°; mm, in],
- zdvih na začátku h 0 [mm, in],
- zdvih na konci h max [mm, in],
- zdvih segmentu d h = h max - h 0 [ mm, in].
Závislosti zdvihu
Rotační a válcová vačka
Úhel rotace vačky ϕ i [°]
Skutečná relativní poloha v segmentu: z i = (ϕ i - L 0 ) / dL (rozsah 0 - 1)
|
Zdvih |
y i = dh f y (z) [mm, in] |
|
Rychlost |
|
|
|
|
|
Zrychlení |
|
|
|
|
|
Puls |
|
|
|
Posuvná vačka
Pozice pohybu vačky L i [mm, in]
Skutečná relativní pozice v segmentu: z i = (L i - L 0 ) / dL (rozsah 0 - 1)
|
Zdvih |
y i = dh f y (z) [mm, in] |
|
Rychlost |
|
|
Zrychlení |
|
|
|
|
|
Puls |
|
|
|
Funkce pohybu
Cykloidní (rozšířená sinusoida)
Tento pohyb má výborné vlastnosti zrychlení. Je často používán pro vysokorychlostní vačky, protože nezpůsobuje velký hluk, vibrace nebo opotřebení.
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
|
Zdvih |
f y (z) = z - 0,5/π sin(2πz) |
|
Rychlost |
f v (z) = 1 - cos (2πz) |
|
Zrychlení |
f a (z) = 2π sin(2πz) |
|
Puls |
f j (z) = 4π 2 cos(2πz) |
Harmonický (sinusoida)
Tato křivka přináší výhodu rovnoměrné rychlosti a zrychlení při záběru. Okamžité změny ve zrychlení na začátku a konci pohybu však často způsobují vibrace, hluk a opotřebení.
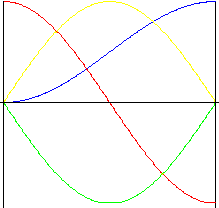
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
|
Zdvih |
f y (z) = 0,5 (1 - cos πz)) |
|
Rychlost |
f v (z) = 0,5 π sin (πz) |
|
Zrychlení |
f a (z) = 0,5 π 2 cos(πz) |
|
Puls |
f j (z) = -0,5π 3 sin(πz) |
Lineární
Jednoduchý pohyb se značným nárazem na začátku a na konci pohybu. S výjimkou velice jednoduchých zařízení se používá vzácně. Doporučujeme použít pohyb s upraveným začátkem a koncem pohybu – parabolický s lineární součástí.
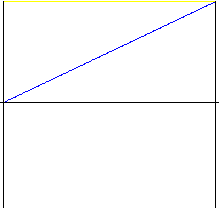
|
|
Zdvih |
|
|
Rychlost |
|
Zdvih |
f y (z) = z |
|
Rychlost |
f v (z) = 1 |
|
Zrychlení |
f a (z) = 0 |
|
Poznámka: Pro z = 0 a z = 1 by měla být správná hodnota hodnotou konečnou, ale výpočet nemůže pracovat s konečnými hodnotami a používá hodnotu nulovou.
|
|
|
Puls |
f j (z) = 0 |
|
Poznámka: Pro z = 0 a z = 1 by měla být správná hodnota hodnotou konečnou, ale výpočet nemůže pracovat s konečnými hodnotami a používá hodnotu nulovou.
|
Parabola (polynom 2. stupně)
Pohyb s nejmenším možným zrychlením. Okamžité změny ve zrychlení na začátku, během i na konci pohybu však často způsobují rázy. Zpětný převod umožňuje „prodloužení“ střední části pohybu a tím také změnu poměru zrychlení a zpomalení.
symetrický (zpětný převod k r = 0,5)
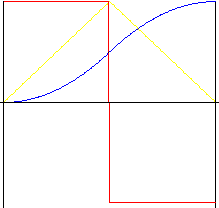
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
for z = 0 to 0,5: |
|||
|
Zdvih |
fy(z) = 2z 2 |
||
|
Rychlost |
fv(z) = 4z |
||
|
Zrychlení |
fa (z) = 4 |
||
|
Puls |
fa(z) = 0 |
||
|
pro z = 0,5 - 1: |
|||
|
Zdvih |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Rychlost |
fv(z) = 4 (1 - z) |
||
|
Zrychlení |
fa (z) = -4 |
||
|
Puls |
fj(z) = 0 |
||
|
Poznámka: Pro z = 0 a z = 1 by měla být správná hodnota hodnotou konečnou, ale výpočet nemůže pracovat s konečnými hodnotami a používá hodnotu nulovou.
|
|||
neasymetrický
k r – zpětný převod (v rozsahu od 0,01 do 0,99)
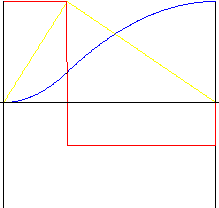
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
pro z = 0 to k r : |
|||
|
Zdvih |
f y (z) = z 2 / k r |
||
|
Rychlost |
f v (z) = 2z / k r |
||
|
Zrychlení |
f a (z) = 2 / k r |
||
|
Puls |
f j (z) = 0 |
||
|
pro z = k r až 1: |
|||
|
Zdvih |
f y (z) = 1 – (1 – z) 2 / (1 – k r ) |
||
|
Rychlost |
f v (z) = 2 (1 – z) / (1 – k r ) |
||
|
Zrychlení |
f a (z) = -2 / (1 - k r ) |
||
|
Puls |
f j (z) = 0 |
||
|
Poznámka: Pro z = 0 a z = 1 by měla být správná hodnota hodnotou konečnou, ale výpočet nemůže pracovat s konečnými hodnotami a používá hodnotu nulovou.
|
|||
Parabolický s lineární částí
Poskytuje přijatelnější zrychlení a zpomalení než pohyb lineární. Zpětný převod umožňuje „prodloužení“ střední části pohybu a tím také změnu poměru zrychlení a zpomalení. Převod lineární části umožňuje nastavit relativní velikost části lineárního pohybu.
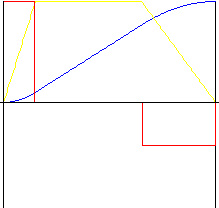
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
k r – zpětný převod (v rozsahu od 0,01 do 0,99)
k l – převod lineární části (v rozsahu od 0,01 do 0,99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
pro z = 0 k k r / k z : |
|||
|
Zdvih |
f y (z) = k h z 2 k z 2 / k r |
||
|
Rychlost |
f v (z) = 2 k h z k z 2 / k r |
||
|
Zrychlení |
f a (z) = 2 k h k z 2 / k r |
||
|
Puls |
f j (z) = 0 |
||
|
pro z = k r / k z k r / k z + k l : |
|||
|
Zdvih |
f y (z) = (z - 0,5 k r / k z ) 2 / (1 + k l ) |
||
|
Rychlost |
f v (z) = 2 / (1 + k l ) |
||
|
Zrychlení |
f a (z) = 0 |
||
|
Puls |
f j (z) = 0 |
||
|
pro z = k r / k z + k l k 1: |
|||
|
Zdvih |
f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Rychlost |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Zrychlení |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Puls |
f j (z) = 0 |
||
Polynom 3. stupně (kubická parabola)
Pohyb s menšími rázy než u pohybu parabolického.
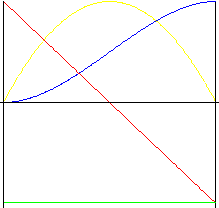
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
|
Zdvih |
f y (z) = (3 -2z) z 2 |
|
Rychlost |
f v (z) = (6 - 6z) z |
|
Zrychlení |
f a (z) = 6 - 12z |
|
Puls |
f j (z) = -12 |
Polynom 4. stupně
Pohyb s menšími rázy než se vyskytují u pohybu s mnohočlenem 3. řádu.
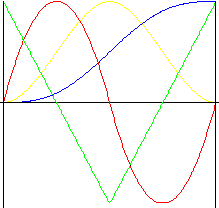
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
|
pro z = 0 - 0,5 |
||
|
Zdvih |
f y (z) = (1 - z) 8z 3 |
|
|
Rychlost |
f v (z) = (24 - 32z) z 2 |
|
|
Zrychlení |
f a (z) = (48 - 96z) z |
|
|
Puls |
f j (z) = 48 - 192z |
|
|
pro z = 0,5 - 1 |
||
|
Zdvih |
f y (z) = 1 - 8z (1 - z) 3 |
|
|
Rychlost |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Zrychlení |
f a (z) = (48 - 96z) (1 - z) |
|
|
Puls |
f j (z) = 194z - 144 |
|
Polynom 5. stupně
Pohyb s menšími rázy než se vyskytují u pohybu s mnohočlenem 3. řádu.
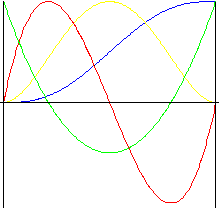
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
|
Zdvih |
f y (z) = (6z 2 - 15z + 10) z 3 |
|
Rychlost |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Zrychlení |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Puls |
f j (z) = (6z 2 - 6z + 1) 60 |
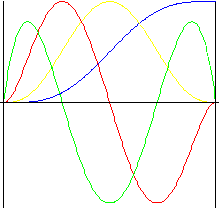
Polynom 7. stupně
Vyrovnanost ve všech vzorcích, včetně pulzů.
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
|
Zdvih |
f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Rychlost |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Zrychlení |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Puls |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
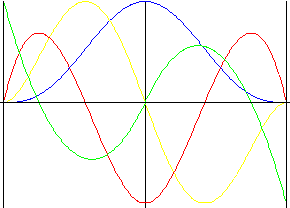
Asymetrický polynom 5. stupně
Podobné jako u mnohočlenu 5. řádu, ale s nuceným obratem zdvihu.
|
|
Zdvih |
|
|
Rychlost |
|
|
Zrychlení |
|
|
Puls |
|
Součást 1 |
||
|
Zdvih |
f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Rychlost |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Zrychlení |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Puls |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Část 2 |
||
|
Zdvih |
f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Rychlost |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Zrychlení |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Puls |
f j (z) = (4z 2 - 3z) 40 |
|
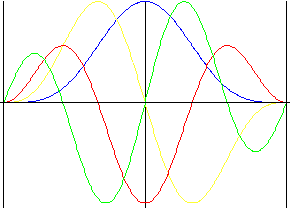
Dvouharmonický
Vyrovnanost ve všech vzorcích včetně pulzů s nuceným obratem zdvihu.
|
Součást 1 |
||
|
Zdvih |
f y (z) = cos(0,5π (1 - z)) 4 |
|
|
Rychlost |
f v (z) = π (0,5 sin(πz) - 0,25 sin(2πz)) |
|
|
Zrychlení |
f a (z) = 0,5 π 2 (cos(πz) - cos(2πz)) |
|
|
Puls |
f j (z) = π 3 (-0,5 sin(πz) + sin(2πz)) |
|
|
Část 2 |
||
|
Zdvih |
f y (z) = 1 - cos(0,5π z) 4 |
|
|
Rychlost |
f v (z) = π (0,5 sin(πz) + 0,25 sin(2πz)) |
|
|
Zrychlení |
f a (z) = 0,5 π 2 (cos(πz) + cos(2πz)) |
|
|
Puls |
f j (z) = -π 3 (0,5 sin(πz) + sin(2πz)) |
|
Porovnání maximálních relativních hodnot
|
Pohyb |
Rychlost |
Zrychlení |
Puls |
|
Cykloidní (rozšířená sinusoida) |
2 |
6,28 |
39,5 |
|
Harmonický (sinusoida) |
1,57 |
4,93 |
15,5 |
|
Lineární |
1 |
∞ |
∞ |
|
Parabolický (mnohočlen 2. řádu) |
2 |
4 |
∞ |
|
Mnohočlen 3. řádu |
1,5 |
6 |
12 |
|
Mnohočlen 4. řádu |
2 |
6 |
48 |
|
Mnohočlen 5. řádu |
1,88 |
5,77 |
60 |
|
Mnohočlen 7. řádu |
2,19 |
7,51 |
52,5 |
|
Asymetrický mnohočlen 5. řádu |
1,73 |
6,67 |
40 |
|
Dvouharmonický |
2,04 |
9,87 |
42,4 |
Další závislosti
Síla na kladce
|
F i = F + m a i + c y i [N, lb] |
Normálová síla
|
Fn i = F i / cos (γ i ) [N, lb] |
Moment
|
T i = F i r i tan (γ i ) [Nmm, lb in] |
Specifický tlak (Hertz)
|
|
|
|
b = min (b v, b k ) |