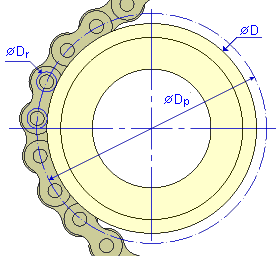
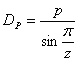Délka řetězu je dána počtem článků řetězu a rozteče řetězu. Dráha řetězového převodu se zakládá na individuální poloze řetězového kola a požadovaného směru pohybu.
Algoritmus výpočtu délky řetězu používá průměry roztečných kružnic řetězových kol. Průměr roztečné kružnice pro každé hnací kolo řetězové kladky nebo napínacího kola řetězu lze získat z níže uvedených rovnic.
Poloha řadicího řetězového kola se patřičně seřídí tak, aby byla splněna požadovaná délka řetězu. Pro zjištění patřičné polohy řadicího řetězového kola se používá řešení pomocí lineární algebry a iterace.
Při výpočtu délky řetězu se zohledňuje skutečnost, že se tato dráha skládá z lineárních úseček o délce rozteče řetězu a oblouky se nahrazují reálnými mnohoúhelníky.
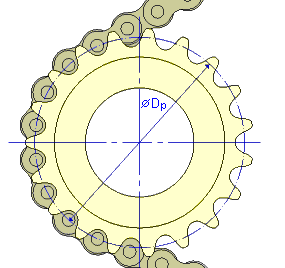
Průměry stoupání
 |
|
|
|
kde: |
||
|
D P |
Průměr roztečné kružnice |
|
|
p |
rozteč řetězu |
|
|
z |
počet zubů řetězového kola |
|
|
|
D p = D + D r |
|
|
kde: |
||
|
D P |
Průměr roztečné kružnice |
|
|
D |
Jmenovitý průměr napínacího kola řetězu |
|
|
D r |
maximální průměr válečku řetězu |
|
Příklad řetězového pohonu se dvěma řetězovými koly
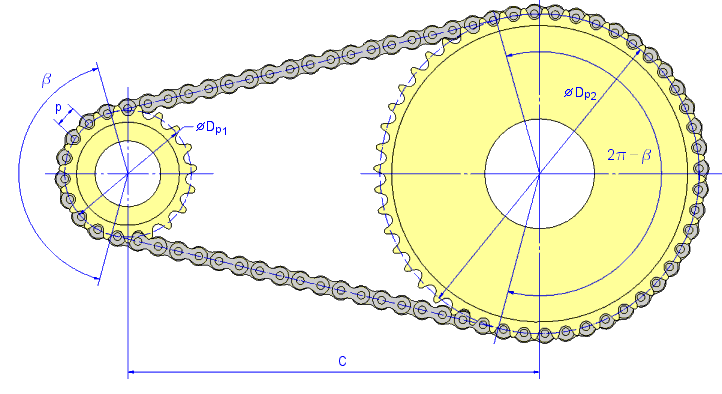
Požadovaný počet článků řetězu pro danou středovou vzdálenost
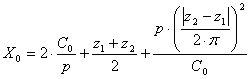
Požadovaný počet článků řetězu se zaokrouhluje na nejbližší sudé nebo liché číslo a potom se skutečná osová vzdálenost určí jako
C = F p [ 2 X - (z 1 + z 2 )]
kde:
|
|
|
|
|
Styčný úhel se potom určí jako
|
|
Počet zubů ve styku s malým řetězovým kolem
|
|
Význam použitých proměnných:
|
C 0 |
Požadovaná osová vzdálenost [m] |
|
C |
Skutečná osová vzdálenost [m] |
|
p |
Rozteč řetězu [m] |
|
z 1 |
Počet zubů hnacího řetězového kola [-] |
|
z 2 |
Počet zubů poháněného řetězového kola [-] |
|
D P1 |
Průměr roztečné kružnice hnacího řetězového kola [m] |
|
D P2 |
Průměr roztečné kružnice poháněného řetězového kola [m] |
|
X 0 |
Požadovaný počet článků řetězu [-] |
| β |
Styčný úhel [stupně] |