Tato část obsahuje seznam problémů ověření výsledků Generátoru tvarů. Vždy, když je to možné, je důležité porovnat výsledky Generátoru tvarů se známými nebo teoretickými řešeními, a určit tak, zda lze jeho výsledky spolehlivě použít.
Most
V tomto problému je cílem určit podpůrnou strukturu potřebnou k podpoře jednotně distribuovaného zatížení působícího na plochu. Jak je znázorněno na obrázku níže, v dolní části struktury existují tři pevné vazby [1].
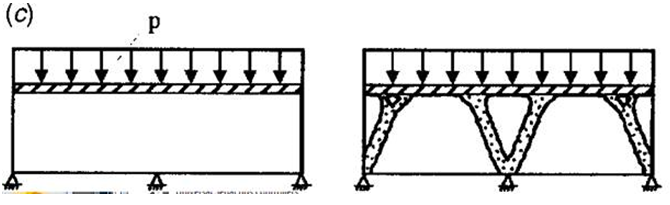
Pomocí Generátoru tvarů tuto strukturu vymodelujeme jako nosník s jednotně distribuovaným zatížením působícím na jeho horní plochu. Tři pevné vazby se použijí u dolní části nosníku, jedna na každé straně a jedna v polovině jeho délky. Níže uvedený výsledek odpovídá publikovanému řešení. Vygenerovaný tvar má formu mostovky na dvou podpůrných obloucích, které přenášejí tlakové zatížení na pevné vazby.
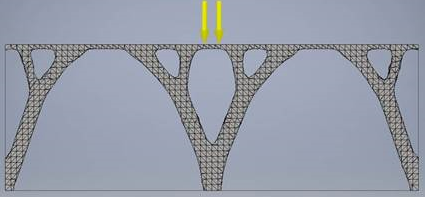
Hemisférická skořepina
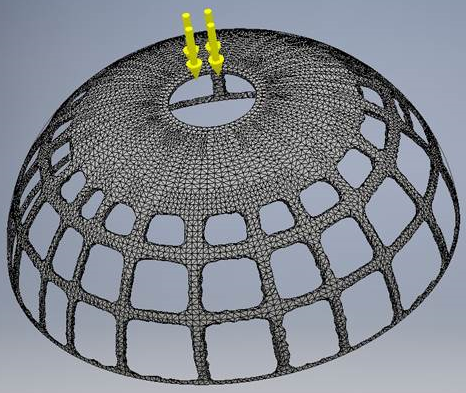
V tomto problému je analyzována tenká hemisférická skořepina. Skořepina má v horní části díru, kolem které je použito tlakové zatížení. Posunutí ve směru osy Y jsou fixována k dolní hraně hemisféry. Posunutí ve směrech os X a Z jsou fixována kolem okrajů díry v horní části hemisféry [2].
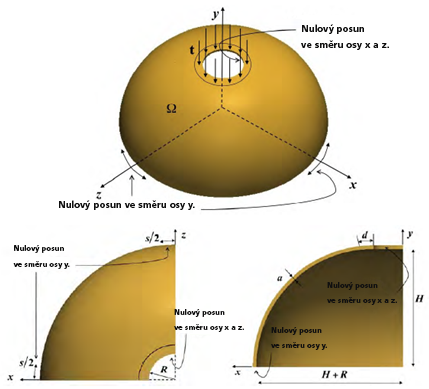
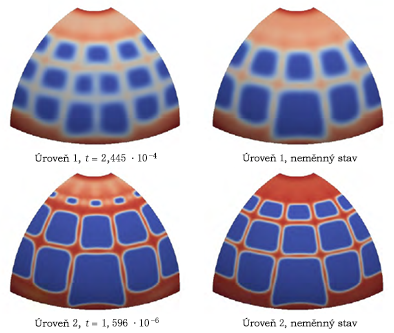

Pomocí Generátor tvarů lze reprodukovat publikovaný výsledek. Ačkoliv se vygenerovaný výsledek shoduje s očekávaným do velké míry, u dolního okraje hemisféry se v některých ohledech liší. Ve výsledku Generátoru tvarů je zachována tenká vrstva materiálu v místě použití omezujících podmínek. Publikované výsledky obsahují mnohem silnější pruh materiálu u dolní hrany hemisféry. Publikované výsledky také obsahují jistou varianci tloušťky tohoto pruhu materiálu, pravděpodobně z důvodu použití omezujících podmínek symetrie.
Reference
- Eschenauer, H.A., and Olhoff, N. (2001). Topology Optimization of Continuum Structures. Journal of Applied Mechanics Reviews. 54(4): 372.
- Dede, L., Borden, M.J., and Hughes, T.J.R. (2012) Isogeometric Analysis for Topology Optimization with a Phase Field Model. Archives of Computational Methods in Engineering. 19(3): 427-465.