Výpočty zkrutných pružin v metrických jednotkách

Obecné výpočtové vzorce

Vnější průměr pružiny

D ₁ = D + d [mm]

kde:

	D	střední průměr pružiny [mm]
	d	průměr drátu [mm]

Vnitřní průměr pružiny

D ₂ = D - d [mm]

kde:

	D	střední průměr pružiny [mm]
	d	průměr drátu [mm]

Krouticí moment pružiny v předpruženém stavu

kde:

	F 1	pracovní síla vyvinutá pružinou ve stavu předpruženém [N]
	R 1	rameno pracovní síly [mm]

Krouticí moment vyvinutý pružinou v plně zatíženém stavu

kde:

	F 8	pracovní síla vyvinutá pružinou ve stavu plně zatíženém [N]
	R 1	rameno pracovní síly [mm]

Index pružiny

c = D/d [-]

kde:

	D	střední průměr pružiny [mm]
	d	průměr drátu [mm]

Úhel pracovního zdvihu

ϕ _h = ϕ ₈ - ϕ ₁ [°]

kde:

	ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]
	ϕ 1	úhlová výchylka pracovního ramene v předpruženém stavu [°]

Minimální úhlová výchylka pracovního ramene

kde:

	M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
	k	krutový poměr pružiny [Nm/°]
	ϕ h	úhel pracovního zdvihu [°]
	M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]

Maximální úhlová výchylka pracovního ramene

kde:

	M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
	k	krutový poměr pružiny [Nm/°]
	ϕ h	úhel pracovního zdvihu [°]
	M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]

Součinitel koncentrace napětí

kde:

	i	Poměr vinutí [-]
	i = D/d [-]	pro výpočet ohybového napětí v činných závitech
		pro výpočet napětí v místě ohybu na rameně
	r	poloměr ohybu na rameně (vnitřní) [mm]
	d	průměr drátu [mm]

Napětí materiálu pružiny obecně

kde:

	M	krouticí moment vyvinutý pružinou obecně [Nm]
	K f	korekční součinitel napětí v ohybu [-]
	d	průměr drátu [mm]

Počet činných závitů pružiny

kde:

	ϕ	úhlová výchylka pracovního ramene obecně [°]
	E	modul pružnosti v tahu [psi]
	d	průměr drátu [mm]
	M	krouticí moment vyvinutý pružinou obecně [Nm]
	R 1	rameno pracovní síly [mm]
	R 2	rameno opěrné síly vyvinuté pružinou [mm]
	D	střední průměr pružiny [mm]

Výpočet návrhu pružiny

Při návrhu pružiny je pro dané zatížení, materiál a montážní rozměry resp. průměr pružiny navržen průměr drátu, počet závitů a pro radiální vyhnutá ramena také poloměr ohybu. Přednostně je pružina navrhována pro doporučené průměry drátu. U pružin s vůlí mezi závity je pružina pokud možno navrhována tak, aby rozteč mezi závity pružiny ve volném stavu byla v doporučeném intervalu 0,3 D ≤ t ≤ 0,5 D [mm].

Návrh pružiny je založen na pevnostní podmínce (σ ₈ ≤ u _s sA), na pevnostní podmínce (σ _8r ≤ u _s σ _A ) a na doporučených rozmezích některých geometrických rozměrů pružiny.

L _Z ≤ 10 D a L _Z ≤ 31,5 palce a 4 ≤ D/d ≤ X a n≥ 1,5 a 1,2 d ≤ t < D a r ≥ d.

kde:

• Pro pružinu s přiléhajícími závity X = 16
• Pro pružinu s vůlí mezi závity X = 10

Rozměry pružiny musí samozřejmě vyhovovat geometricky proveditelnému řešení z hlediska zadaného tvaru a délky ramen. Je-li tak nastaveno v zadání, musí rozměry pružiny dále vyhovovat i mezním rozměrů uložení, tedy maximálnímu dovolenému průměru a délce pouzdra resp. minimálnímu dovolenému průměru trnu.

Dané maximální zatížení, materiál a kóty sestavy pružiny

Nejdříve jsou zkontrolovány a dopočteny vstupní hodnoty výpočtu.

Pro dané max. zatížení a montážní rozměry je dále dopočteno min. zatížení,

kde:

	M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
	M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]
	ϕ 1	úhlová výchylka pracovního ramene v předpruženém stavu [°]
	ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]

Poté je navržen průměr drátu a počet závitů tak, aby po dopočtení průměru pružiny byly splněny pevnostní a geometrické podmínky. Je-li v zadání omezena hodnota průměru pružiny, pak musí návrh pružiny vyhovovat samozřejmě i této podmínce. V opačném případě jsou mezní hranice průměru pružiny dány výše uvedenými geometrickými podmínkami pro minimální a maximální přípustný průměr drátu.

Pro pružinu s radiálními vyhnutými rameny navrhne program dále vyhovující poloměry ohybu ramen.

Program při návrhu postupně prochází od nejmenšího k největšímu všechny pevnostně a geometricky vyhovující průměry drátu pružiny. Potom testuje pro jednotlivé vyhovující počty závitů, zda takto navržená pružina odpovídá všem požadovaným podmínkám. V takovém případě je návrh ukončen se zvolenými hodnotami, bez ohledu na další vyhovující průměry drátu pružiny. Program se tedy snaží navrhnout pružinu s co nejmenším průměrem drátu a co nejmenším počtem závitů a průměrem pružiny.

Dané zatížení, materiál a úhel pracovního vychýlení

Nejprve se zkontrolují vstupní hodnoty pro výpočet.

Pro dané zatížení a úhel pracovního zdvihu jsou dále dopočteny úhlové výchylky pracovního ramena.

Minimální výchylka pracovního ramene

Maximální výchylka pracovního ramene

kde:

	M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
	M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]
	ϕ 1	úhlová výchylka pracovního ramene v předpruženém stavu [°]
	ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]
	ϕ h	úhel pracovního zdvihu [°]

Poté je navržen průměr drátu a počet závitů tak, aby po dopočtení průměru pružiny byly splněny pevnostní a geometrické podmínky. Je-li v zadání omezena hodnota průměru pružiny, pak musí návrh pružiny vyhovovat samozřejmě i této podmínce. V opačném případě jsou mezní hranice průměru pružiny dány výše uvedenými geometrickými podmínkami pro minimální a maximální přípustný průměr drátu.

Pro pružinu s radiálními vyhnutými rameny navrhne program dále vyhovující poloměry ohybu ramen.

Program při návrhu postupně prochází od nejmenšího k největšímu všechny pevnostně a geometricky vyhovující průměry drátu pružiny. Dále testuje pro jednotlivé vyhovující počty závitů, zda takto navržená pružina odpovídá všem požadovaným podmínkám. V takovém případě je návrh ukončen se zvolenými hodnotami, bez ohledu na další vyhovující průměry drátu pružiny. Program se tedy snaží navrhnout pružinu s co nejmenším průměrem drátu a co nejmenším počtem závitů a průměrem pružiny.

Dané maximální zatížení, materiál a průměr pružiny

Nejprve se zkontrolují vstupní hodnoty pro výpočet.

Dále je navržen průměr drátu, počet závitů a kóty sestavy tak, aby byly splněny pevnostní a geometrické podmínky. Je-li v zadání omezena hodnota úhlu pracovního zdvihu pružiny, pak musí návrh pružiny vyhovovat samozřejmě i této podmínce. V opačném případě jsou mezní hranice kót sestavy dány geometrickými podmínkami pro zadaný průměr pružiny a minimální resp. maximální přípustný průměr drátu.

Pro pružinu s radiálními vyhnutými rameny, navrhne program dále vyhovující poloměry ohybu ramen.

Program při návrhu postupně prochází od nejmenšího k největšímu všechny pevnostně a geometricky vyhovující průměry drátu pružiny. Dále testuje pro všechny jednotlivé počty závitů, zda takto navržená pružina odpovídá všem požadovaným podmínkám. V takovém případě je návrh ukončen se zvolenými hodnotami, bez ohledu na další vyhovující průměry drátu pružiny. Program se tedy snaží navrhnout pružinu s co nejmenším průměrem drátu a co nejmenším počtem závitů a průměrem pružiny.

Dané maximální zatížení, materiál, průměr pružiny a úhel pracovního vychýlení

Nejprve se zkontrolují vstupní hodnoty pro výpočet.

Dále je navržen průměr drátu, počet závitů a úhlové výchylky pracovního ramena tak, aby byly splněny uvedené pevnostní a geometrické podmínky. Program vyhledá co nejmenší maximální úhlovou výchylku pracovního ramene ϕ ₈ tak, aby se hodnota minimální úhlové výchylky pracovního ramene ϕ ₁ rovnala přibližně 2°.

Pro pružinu s radiálními vyhnutými rameny navrhne program dále vyhovující poloměry ohybu ramen.

Na závěr je pro dané maximální zatížení a navržené úhlové výchylky pracovního ramena dopočteno min. zatížení pružiny:

kde:

	M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
	M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]
	ϕ 1	úhlová výchylka pracovního ramene v předpruženém stavu [°]
	ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]

Program při návrhu postupně prochází od nejmenšího k největšímu všechny pevnostně a geometricky vyhovující průměry drátu pružiny a testuje pro jednotlivé vyhovující počty závitů zda takto navržená pružina odpovídá všem požadovaným podmínkám. V takovém případě je návrh ukončen se zvolenými hodnotami, bez ohledu na další vyhovující průměry drátu pružiny. Program se tedy snaží navrhnout pružinu s co nejmenším průměrem drátu a co nejmenším počtem závitů a průměrem pružiny.

Kontrolní výpočet pružiny

Vypočítá odpovídající hodnoty montážních rozměrů pro dané zatížení, materiál a rozměry pružiny. Nejdříve jsou zkontrolovány a dopočteny vstupní údaje, montážní rozměry jsou počítány dle následujících vztahů.

Minimální úhlová výchylka pracovního ramene

kde:

	M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
	D	střední průměr pružiny [mm]
	n	počet činných závitů [-]
	R 1	rameno pracovní síly [mm]
	R 2	rameno opěrné síly vyvinuté pružinou [mm]
	E	modul pružnosti [MPa]
	d	průměr drátu [mm]

Maximální úhlová výchylka pracovního ramene

kde:

	M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]
	D	střední průměr pružiny [mm]
	n	počet činných závitů [-]
	R 1	rameno pracovní síly [mm]
	R 2	rameno opěrné síly vyvinuté pružinou [mm]
	E	modul pružnosti [MPa]
	d	průměr drátu [mm]

Úhel pracovního zdvihu

ϕ _h = ϕ ₈ - ϕ ₁ [°]

kde:

M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]
ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]

Výpočet pracovních sil

V tomto výpočtu jsou pro daný materiál, montážní rozměry a rozměry pružiny dopočteny odpovídající síly vyvinuté pružinou v jednotlivých pracovních stavech pružiny. Nejdříve jsou zkontrolovány a dopočteny vstupní údaje, pracovní síly jsou počítány dle následujících vztahů.

Minimální pracovní zatížení

kde:

	M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
	D	střední průměr pružiny [mm]
	n	počet činných závitů [-]
	R 1	rameno pracovní síly [mm]
	R 2	rameno opěrné síly vyvinuté pružinou [mm]
	E	modul pružnosti [MPa]
	d	průměr drátu [mm]
	ϕ 1	úhlová výchylka pracovního ramene v předpruženém stavu [°]

Maximální pracovní zatížení

kde:

	M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]
	D	střední průměr pružiny [mm]
	n	počet činných závitů [-]
	R 1	rameno pracovní síly [mm]
	R 2	rameno opěrné síly vyvinuté pružinou [mm]
	E	modul pružnosti [MPa]
	d	průměr drátu [mm]
	ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]

Výpočet výstupních parametrů pružiny

Tato část je společná pro všechny typy výpočtu pružiny a provádí se v následujícím pořadí.

Krutový poměr pružiny

Prostor mezi závity volné pružiny

a = t - d [mm]

Délka části pružiny tvořená závity u volné pružiny

pro pružinu s přiléhajícími závity
	L 0 = (1.05 n + 1) d [mm]
pro pružinu s vůlí mezi závity
	L 0 = t n + d [mm]

Napětí materiálu pružiny v ohybu v činných závitech při minimálním pracovním zatížení

kde je součinitel koncentrace napětí K _f vypočten pro i = D/d

Ohybové napětí materiálu pružiny v místě ohybu na rameni při minimálním pracovním zatížení

kde je součinitel koncentrace napětí K _f vypočten pro i = 2r/d + 1

Ohybové napětí materiálu pružiny v činných závitech v plně zatíženém stavu

kde je součinitel koncentrace napětí K _f vypočten pro i = D/d

Ohybové napětí materiálu pružiny v místě ohybu na rameni v plně zatíženém stavu

kde je součinitel koncentrace napětí K _f vypočten pro i = 2r/d + 1

Délka části pružiny tvořená závity v plně zatíženém stavu u pružiny s přiléhajícími závity zatížené ve svinování

Vnější průměr pružiny v plně zatíženém stavu u pružiny zatížené ve svinování

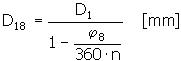
Vnitřní průměr pružiny v plně zatíženém stavu u pružiny zatížené ve svinování

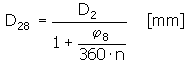
Mezní zkušební úhlová výchylka pracovního ramene

Deformační energie pružiny

Délka drátu

l = 3,2 D n + l R [mm]
kde l R je délka ramene, zatímco:
	kde l R je délka ramene, zatímco:
			délka tangenciálního ramena
			délka radiálního vyhnutého ramena

Hmotnost pružiny

Kontrola zatížení pružiny

(σ ₈ ≤ u _s σ _A ) a (σ _8r ≤ u _s σ _A )

Význam použitých proměnných:

a	vůle mezi činnými závity ve volném stavu [mm]
d	průměr drátu [mm]
D	střední průměr pružiny [mm]
D 1	vnější průměr pružiny [mm]
D 2	vnitřní průměr pružiny [mm]
E	modul pružnosti v tahu [psi]
F	pracovní síla vyvinutá pružinou (síla vyvinutá na rameni R 1 pracovní síly), obecně [N]
i	poměr vinutí [-]
K F	korekční součinitel napětí v ohybu [-]
kϕ	krutový poměr pružiny [Nm/°]
r 1	poloměr ohybu na pracovním rameně [mm]
r 2	poloměr ohybu na opěrném rameně [mm]
R 1	rameno pracovní síly [mm]
R 2 1	rameno opěrné síly vyvinuté pružinou [mm]
l	délka drátu [mm]
L 0	délka části tvořené závity u pružiny ve volném stavu obecně [mm]
m	hmotnost pružiny [N]
M	krouticí moment vyvinutý pružinou obecně [Nm]
n	počet činných závitů [-]
t	rozteč činných závitů (stoupání) ve volném stavu [mm]
u s	součinitel využití materiálu
ρ	hustota materiálu pružiny [lb/ft3]
ϕ	úhlová výchylka pracovního ramene obecně [°]
σ	napětí materiálu pružiny v ohybu obecně [psi]
σ A	dovolené napětí materiálu pružiny v ohybu [psi]
M 1	krouticí moment pružiny ve stavu předpruženém [Nm]
M 8	krouticí moment vyvinutý pružinou ve stavu plně zatíženém [Nm]
ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]
ϕ 1	úhlová výchylka pracovního ramene v předpruženém stavu [°]
ϕ 8	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]
ϕ h	úhlová výchylka pracovního ramene u plně zatížené pružiny [°]