Obecné výpočtové vzorce
Vnější průměr pružiny
D 1 = D + d [mm]
kde:
|
D |
střední průměr pružiny [mm] |
|
|
d |
průměr drátu [mm] |
Vnitřní průměr pružiny
D 2 = D - d [mm]
kde:
|
D |
střední průměr pružiny [mm] |
|
|
d |
průměr drátu [mm] |
Pracovní vychýlení
H = L 8 - L 1 = s 8 - s 1 [mm]
kde:
|
L 8 |
délka plně zatížené pružiny [mm] |
|
|
L 1 |
délka předpružené pružiny [mm] |
|
|
s 8 |
deformace plně zatížené pružiny [mm] |
|
|
s 1 |
deformace předpružené pružiny [mm] |
Výška oka pružiny
![]()
kde:
|
L 0 |
délka volné pružiny [mm] |
|
|
L Z |
délka části pružiny tvořená závity [mm] |
Index pružiny
c = D/d [-]
kde:
|
D |
střední průměr pružiny [mm] |
|
|
d |
průměr drátu [mm] |
Wahlův korekční součinitel
![]()
kde:
|
c |
poměr vinutí [-] |
|
|
L Z |
délka části pružiny tvořená závity [mm] |
Počáteční napětí
![]()
kde:
|
d |
průměr drátu [mm] |
|
|
τ 0 |
napětí ve stavu volném [MPa] |
|
|
D |
střední průměr pružiny [mm] |
|
|
K w |
korekční součinitel Wahl [-] |
Celková síla vyvinutá pružinou
![]()
kde:
|
d |
průměr drátu [mm] |
|
| τ |
napětí v krutu je síla na jednotku plochy. materiálu pružiny obecně [MPa] |
|
|
D |
střední průměr pružiny [mm] |
|
|
K w |
korekční součinitel Wahl [-] |
|
|
G |
modul pružnosti materiálu pružiny [MPa] |
Konstanta pružiny
![]()
kde:
|
d |
průměr drátu [mm] |
|
|
G |
modul pružnosti materiálu pružiny [MPa] |
|
|
D |
střední průměr pružiny [mm] |
|
|
n |
počet činných závitů [-] |
|
|
F 8 |
pracovní síla plně zatížené pružiny [MPa] |
|
|
F 1 |
pracovní síla minimálně zatížené pružiny [MPa] |
|
|
H |
pracovní zdvih [mm] |
Výpočet návrhu pružiny
Při návrhu pružiny je pro dané zatížení, materiál a kóty sestavy navržen průměr drátu, počet závitů a délka pružiny ve volném stavu L 0 .
![]()
Pokud vypočtená pružina neodpovídá žádnému průměru drátu pro zatížení τ 0 podle vzorce, bude výpočet pružiny zopakován s opravenou hodnotou napětí ve volném stavu v rámci doporučeného rozpětí.
![]()
Pružina bez předpětí je navržená pro doporučenou střední hodnotu rozteče t = 0.35 D [mm].
Jestliže vypočtená pružina neodpovídá žádnému průměru drátu vybrané rozteče, bude výpočet pružiny zopakován s opravenou hodnotou rozteče v doporučeném rozsahu 0,3 D ≤ t ≤ 0,4 D [mm].
Návrh pružiny je založen na pevnostní podmínce τ 8 ≤ u s τ A a doporučených rozmezí některých geometrických kót pružiny: L 0 ≤ D a L 0 ≤ 31,5 palce a 4 ≤ D/d ≤ 16 a n ≥ 2.
Dané zatížení, materiál a kóty sestavy pružiny
Nejdříve jsou zkontrolovány a dopočteny vstupní hodnoty výpočtu.
Dále je dopočtena délka pružiny ve stavu volném.
![]()
Po výpočtu jsou průměr drátu, počet závitů a délka volné pružiny navrženy tak, aby výška závěsného oka pružiny odpovídala zvolenému typu oka. Musí být také dodržena dříve uvedená pevnost a geometrické podmínky. Je-li v zadání omezena hodnota průměru pružiny, pak musí návrh pružiny vyhovovat samozřejmě i této podmínce. V opačném případě jsou mezní hranice průměru pružiny dány výše uvedenými geometrickými podmínkami pro minimální a maximální přípustný průměr drátu.
Program při návrhu postupně prochází všechny pevnostně a geometricky vyhovující průměry drátu pružiny od nejmenšího k největšímu. Testuje se výška závěsného oka pružiny a počet závitů. V takovém případě je návrh ukončen se zvolenými hodnotami, bez ohledu na další vyhovující průměry drátu pružiny. Program se tedy snaží navrhnout pružinu s co nejmenším průměrem drátu a co nejmenším počtem závitů.
Vypočtená výška oka pružiny musí ležet v rozmezí d ≤ o ≤ 30 d. Musí být nalezena taková kombinace průměru drátu, počtu závitů a průměru pružiny, aby vypočtená výška závěsného oka odpovídala některému ze základních typů ok. Základní typ oka se vybere nejdříve prozkoumáním obyčejného oka, vmáčknutého oka a potom ostatních typů ok.
Určené zatížení, materiál a průměr pružiny
Nejprve se zkontrolují vstupní hodnoty pro výpočet.
Po kontrole je navržen průměr drátu, počet závitů, délka volné pružiny a kóty sestavy tak, aby výška závěsného oka pružiny odpovídala zvolenému typu oka. Musí být také dodrženy pevnostní a geometrické podmínky. Je-li v zadání uveden některý z montážních rozměrů L 1 , L 8 resp. omezena hodnota pracovní deformace pružiny, návrh pružiny potom musí vyhovovat samozřejmě i této podmínce. V opačném případě jsou mezní hranice kót sestavy a délky volné pružiny dány geometrickými podmínkami pro zadaný průměr pružiny a minimálním resp. maximálním přípustným průměrem drátu.
Vzorec návrhu pružiny se zadaným průměrem drátu.
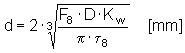
kde je hodnota τ 8 = 0,85 τ A použita pro hodnotu napětí v krutu pro materiál pružiny, v plně zatíženém stavu pružiny.
V případě kdy pro tento průměr drátu není možné navrhnout žádnou vyhovující kombinaci rozměrů pružiny, prochází program při dalším návrhu postupně od nejmenšího k největšímu všechny pevnostně a geometricky vyhovující průměry drátu pružiny. Proběhne testování počtu závitů od nejmenšího po největší, výsledkem kterého je výška oka pružiny splňující podmínky Program se tedy v tomto případě snaží navrhnout pružinu s co nejmenším průměrem drátu a co nejmenším počtem závitů.
Vypočtená výška oka pružiny musí ležet v rozmezí d ≤ o ≤ 30 d. Pro takto vypočtenou výšku oka je zvolen odpovídající typ závěsného oka. Kombinace průměru drátu, počtu závitů, délky volné pružiny a montážních rozměrů musí být taková, aby vypočtená výška závěsného oka odpovídala některému ze základních typů ok. Základní typ oka se vybere nejdříve prozkoumáním obyčejného oka, vmáčknutého oka a potom ostatních typů ok.
Daná maximální pracovní síla, známý materiál, kóty sestavy a průměr pružiny
Nejdříve jsou zkontrolovány a dopočteny vstupní hodnoty výpočtu.
Dále jsou navrženy průměr drátu, počet závitů, délka volné pružiny a minimální pracovní síla F 1 . Kromě splnění výše uvedených pevnostních a geometrických podmínek musí vyhovovat i výška závěsného oka pružiny zvolenému typu oka. Musí být také dodrženy pevnostní a geometrické podmínky.
Vzorec návrhu pružiny se zadaným průměrem drátu.
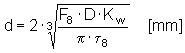
kde je hodnota τ 8 = 0,9 τ A použita pro hodnotu napětí v krutu pro materiál pružiny, v plně zatíženém stavu pružiny.
V případě kdy pro tento průměr drátu není možné navrhnout žádnou vyhovující kombinaci rozměrů pružiny, prochází program při dalším návrhu postupně od nejmenšího k největšímu všechny pevnostně a geometricky vyhovující průměry drátu pružiny. Proběhne testování počtu závitů od nejmenšího po největší, výsledkem kterého je výška oka pružiny splňující podmínky Program se tedy v tomto případě snaží navrhnout pružinu s co nejmenším průměrem drátu a co nejmenším počtem závitů.
Kontrolní výpočet pružiny
Vypočítá odpovídající hodnoty montážních rozměrů a pracovní zdvih pro dané zatížení, materiál a rozměry pružiny.
Nejprve se zkontrolují vstupní hodnoty pro výpočet. Podle následujících vztahů jsou spočítány montážní rozměry.
Délka pružiny s předpětím
![]()
Délka plně zatížené pružiny
![]()
kde:
|
L 0 |
délka volné pružiny [mm] |
|
|
F 1 |
pracovní síla minimálně zatížené pružiny [mm] |
|
|
D |
střední průměr pružiny [mm] |
|
|
n |
počet činných závitů [-] |
|
|
G |
modul pružnosti materiálu pružiny [MPa] |
|
|
d |
průměr drátu [mm] |
|
|
F 8 |
pracovní síla plně zatížené pružiny [MPa] |
Pracovní vychýlení
H = L 1 - L 8 [mm]
Výpočet pracovních sil
Vypočítá pro daný materiál, montážní rozměry a rozměry pružiny odpovídající síly vyvinuté pružinami v jejich provozních stavech. Nejprve se zkontrolují a vypočítají vstupní hodnoty a potom se pomocí následujících vzorců vypočítají pracovní síly.
Minimální pracovní síla
![]()
Maximální pracovní síla
![]()
Výpočet výstupních parametrů pružiny
Tato část je společná pro všechny typy výpočtu pružiny a provádí se v následujícím pořadí.
Součinitel výšky oka
![]()
Konstanta pružiny
![]()
Délka části pružiny tvořené závity
|
pro pružinu bez předpětí |
|
|
L z = t n + d [mm] |
|
|
pro pružinu s předpětím |
|
|
L z = 1,03 (n + 1) d [mm] |
|
Vychýlení předpružené pružiny
s 1 = L 1 - L 0 [mm]
Celkové vychýlení pružiny
s 8 = L 8 - L 0 [mm]
Napětí materiálu předpružené pružiny v krutu
![]()
Napětí materiálu pružiny v krutu v plně zatíženém stavu
![]()
Mezní síla pružiny
![]()
Vychýlení v mezním stavu
![]()
kde:
|
k |
tuhost pružiny [N/mm] |
|
|
F 9 |
pracovní síla pružiny při mezním zatížení [N] |
|
|
F 0 |
předpětí pružiny [N] |
Mezní délka pružiny
L 9 = L 0 + s 9 [mm]
Deformační energie pružiny
![]()
Rozvinutá délka drátu
|
l = 3,2 D n + l 0 [mm] |
|||
|
Kde rozvinutá délka ok l 0 : |
|||
|
pro poloviční oko |
|||
|
l 0 = π D + 4 o - 2 D - 2 d [mm] |
|||
|
pro plné oko |
|||
|
l 0 = 2 (π D - 2 d) [mm] |
|||
|
pro vmáčknuté oko |
|||
|
l 0 = 2 (π D - 2 d) [mm] |
|||
|
pro vmáčknuté oko |
|||
|
l 0 = 2 (π D - d) [mm] |
|||
|
pro hákové oko |
|||
|
l 0 = π D + 2 o - D + 3 d [mm] |
|||
|
pro obyčejné oko dvojité |
|||
|
l 0 = 4 π D [mm] |
|||
|
pro obyčejné oko dvojité nevstředěné |
|||
|
l 0 = 4 π D [mm] |
|||
|
pro neupřesněný typ oka |
|||
|
l 0 = 0 [mm] |
|||
Hmotnost pružiny
![]()
Přirozený kmitočet rázů v pružině
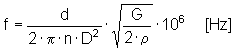
Kontrola zatížení pružiny
τ 8 ≤ u s τ A
Přehled použitých proměnných:
|
d |
průměr drátu [mm] |
|
k |
tuhost pružiny [N/mm] |
|
D |
střední průměr pružiny [mm] |
|
D 1 |
vnější průměr pružiny [mm] |
|
D 2 |
vnitřní průměr pružiny [mm] |
|
F |
pracovní síla vyvinutá pružinou obecně [N] |
|
G |
modul pružnosti materiálu pružiny [MPa] |
|
H |
pracovní zdvih [mm] |
|
c |
poměr vinutí [-] |
|
K w |
korekční součinitel Wahl [-] |
|
l |
rozvinutá délka drátu [mm] |
|
L |
délka pružiny obecně [mm] |
|
L Z |
délka části pružiny tvořená závity [mm] |
|
m |
hmotnost pružiny [N] |
|
n |
počet činných závitů [-] |
|
o |
výška závěsného oka pružiny [mm] |
|
t |
rozteč činných závitů ve volném stavu [mm] |
|
s |
deformace (natažení) pružiny obecně [mm] |
|
u s |
|
| ρ |
hustota materiálu pružiny [N/mm 3 ] |
| τ |
napětí v krutu je síla na jednotku plochy. materiálu pružiny obecně [MPa] |
|
τ A |
dovolené napětí materiálu pružiny v krutu [MPa] |