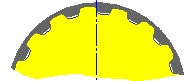
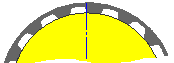
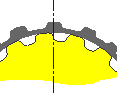
Die Teilriemenlänge ergibt sich aus der Anzahl der Riemenzähne und aus der Zahnkreisteilung. Die Bewegungsbahn des Riemens basiert auf der jeweiligen Riemenscheibenposition. Der Teilkreisdurchmesser (Flankendurchmesser) wird bei jeder Riemenscheibe mithilfe der unten aufgeführten Gleichungen berechnet. Die Position des Schieberads wird entsprechend den Kriterien für die standardmäßige Riemenlänge angepasst. Bei der Berechnung wird mittels Iterationslösung eine geeignete Schieberadposition gefunden, die der angestrebten Position des Schieberads möglichst nahe kommt.
Genauen Flankendurchmesser bestimmen
|
|
Synchrone Riemenscheibe im Uhrzeigersinn oder beidseitiger Riemen |
|
|
|
|
|
Flache Riemenscheibe im Uhrzeigersinn oder beidseitiger Riemen |
|
D p = D + 2(a + h t ) |
|
|
|
Synchrone Riemenscheibe gegen den Uhrzeigersinn und einseitiger Riemen |
|
D p = D 0 + 2(H - a - h t ) |
|
|
|
Flache Riemenscheibe gegen den Uhrzeigersinn und einseitiger Riemen |
|
D p = D + 2(H - a - h t ) |
Beispiel einer Leistungsübertragung mit zwei Riemenscheiben
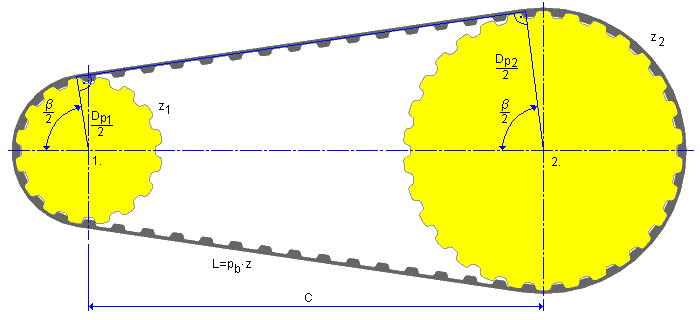
Umspannungswinkel
![]()
Teilriemenlänge
![]()
Achsabstand
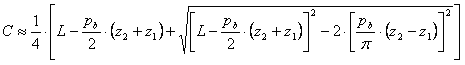
Die folgende Formel empfiehlt sich für die Bestimmung des Achsabstands bei einem neuen Getriebe:
0.2 p b (z 1 + z 2 ) ≤ C ≤ 0.7 p b (z 1 = z 2 )
Bedeutung der verwendeten Variablen:
|
Z |
Anzahl der Zähne der jeweiligen Riemenscheibe / Anzahl der Riemenzähne [-] |
|
p b |
Zahnkreisteilung [m] |
|
D |
Nenndurchmesser der flachen Riemenscheibe [m] |
|
a |
Teillinienversatz [m] |
|
h t |
Riemenzahnhöhe [m] |
|
D 0 |
Außendurchmesser der synchronen Riemenscheibe [m] |
|
H |
Riemenhöhe [m] |
|
C |
Achsabstand der jeweiligen Riemenscheibe und antreibenden Riemenscheibe [m] |
| β |
Umspannungswinkel [°] |