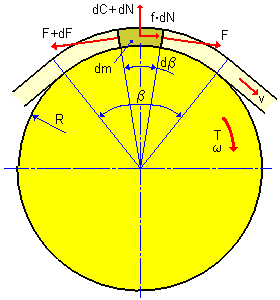
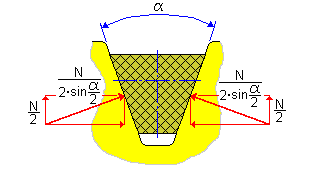
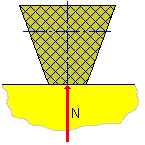
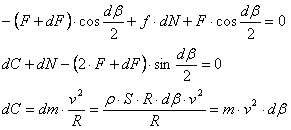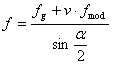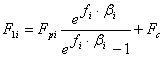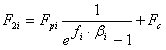Verwendete allgemeine Gleichungen
|
|
|
|
Dabei gilt: m ist eine spezifische Masse des Riemens, definiert als m = S ρ |
Geänderter Reibungskoeffizient der jeweiligen Riemenscheibe
|
|
|
|
|
f = f g + v f mod |
Fundamentale Gleichungen für antreibende Riemenscheibe und Riemen
Zu übertragende Leistung
![]()
Riemengeschwindigkeit
![]()
Riemenbiegefrequenz
![]()
Riemenzugkraft (oder effektive Spannung)
![]()
Zentrifugalkraft
Fc = z m v 2
Spannung in Riemenabschnitten
Mit den folgenden Gleichungen wird von der Anwendung zunächst die Riemenscheibe bestimmt, die als am problematischsten eingeschätzt wird. Zum Übertragen einer Belastung ist hier der maximale Riemeninstallationszug erforderlich. Anschließend wird für alle Riemenscheiben die Riemenspannung in jedem Abschnitt entsprechend angepasst. Ausgangspunkt ist dabei der anfängliche Riemeninstallationszug.
|
|
|
|
F 1i - F p P xi - F 2i = 0 |
|
|
|
|
|
|
Kriterium für die als am problematischsten eingeschätzte Riemenscheibe ist die maximale Spannung der gespannten Seite:
F 1max = max (F 1i )
Der Maximalzug in der Riemenspannung insgesamt (pro Riemen) bei voller Belastung des Riemengetriebes wird wie folgt bestimmt:
![]()
Dabei steht der Ausdruck "k 1 F 1max " der tatsächliche Maximalzug in Riemenspannung, der für alle Riemen in dem Riemenantrieb berücksichtigt wird. Auf diese Weise wird der Zug in einzelnen Spannungen neu berechnet, sodass die folgenden Bedingungen erfüllt sind:
F 1i - F P P xi - F 2i = 0
Resultierende Achsenbelastung für jede Riemenscheibe bei voller Belastung des Riemengetriebes:
![]()
![]()
Anfänglicher Riemeninstallationszug und statische Zugkraft
Der erforderliche anfängliche Riemeninstallationszug (pro Riemen) kann über den Zugkoeffizienten angepasst und wie folgt bestimmt werden:
![]()
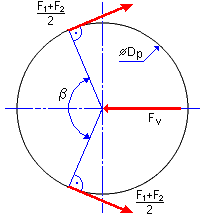
Die statische Spannkraft F v wird für jede Rolle ermittelt. Die Anwendung ermittelt die Spannkraft, die sich entlang der Mittellinien des Riemens aufbaut, wie folgt:
|
|
|
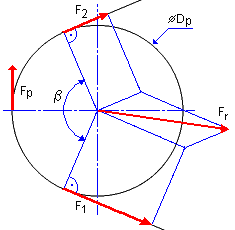
Bedeutung der verwendeten Variablen:
| F | Tangentialkraft [N] |
| β | Umspannungswinkel [°] |
| α | Eckenwinkel [°] |
| C | Zentrifugalkraft [N] |
| N | Normalkraft [N] |
| m | Spezifisches Riemengewicht [kg/m] |
| v | Riemengeschwindigkeit [m/s] |
| R | Riemenscheibenradius [m] |
| S | Riemenquerschnittsfläche [m 2 ] |
| T | Auf die jeweilige Riemenscheibe einwirkendes Drehmoment [Nm] |
| D p | Teilkreisdurchmesser der Riemenscheibe [m] |
| k | Anzahl der Riemenscheiben [-] |
| P | Zu übertragende Leistung [N] |
| v | Riemengeschwindigkeit [m/s] |
| F c | Zentrifugalkraft [N] |
| F 1 | Spannung im Riemenabschnitt bei Eingabe für die jeweilige Riemenscheibe [-] |
| F 2 | Spannung im Riemenabschnitt bei Ausgabe für die jeweilige Riemenscheibe [-] |
| f | Geänderter Reibungskoeffizient der jeweiligen Riemenscheibe [-] |
| P x | Leistungsverhältnis der jeweiligen Riemenscheibe [-] |
| f g | Reibungskoeffizient des jeweiligen Riemenscheibenmaterials und Riemens [-] |
|
f mod |
Drehzahlkoeffizient der Reibungsänderung [s/m] |
| Z | Anzahl der Riemen [-] |
| ρ | Riemendichte [kg/m3] |
| F t | Anfänglicher Riemeninstallationszug [N] |
| F v | Statische Zugkraft für die jeweilige Riemenscheibe [N] |
| k 1 | Zugkoeffizient des Riemens [-] |