Die Riemenlänge wird in einem Bezugssystem oder effektiven System bestimmt. Aus diesem Grund wird zunächst für jede Riemenscheibe der Bezugsdurchmesser oder effektive Durchmesser bestimmt. Die Bewegungsbahn des Riemens basiert auf der jeweiligen Riemenscheibenposition. Die Position des Schieberads wird entsprechend den Kriterien für die standardmäßige Riemenlänge angepasst. Bei der Berechnung wird mittels Iterationslösung eine geeignete Schieberadposition gefunden, die der angestrebten (oder aktuellen) Position des Schieberads möglichst nahe kommt.
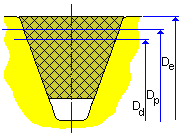
Riemenscheibendurchmesser
|
|
Rillenriemenscheibe |
|
D e = D w + 2 h w |
|
|
D p = D w + 2 a |
|
|
D d = D w |
|
|
|
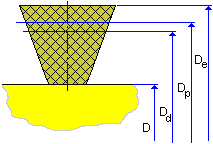
Flache Riemenscheibe, Richtung im Uhrzeigersinn |
|
D e = D + 2 h |
|
|
D p = D + 2 (h - h w + a) |
|
|
D d = D + 2(h - h w ) |
|
|
|
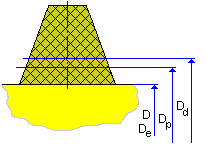
Flache Riemenscheibe, Richtung gegen den Uhrzeigersinn |
|
D e = D |
|
|
D p = D + 2 (h w - a) |
|
|
D d = D + 2 h w |
Beispiel einer Leistungsübertragung mit zwei Riemenscheiben
In diesem Beispiel wird ein Bezugssystem verwendet.
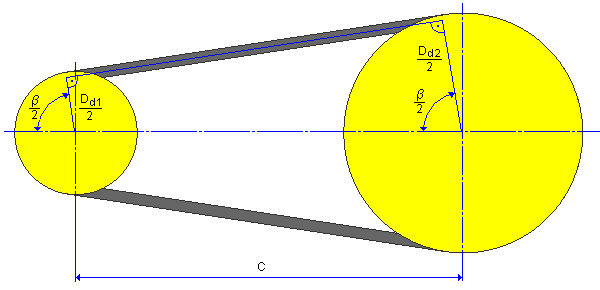
Umspannungswinkel
![]()
Bezugslänge der Riemenscheibe
![]()
Achsabstand
![]()
Die folgende Formel empfiehlt sich für die Bestimmung des Achsabstands bei einem neuen Getriebe:
0.7 (D d1 + D d2 ) ≤ C ≤ 2(D d1 + D d2 )
Bedeutung der verwendeten Variablen:
|
D W |
Nenndurchmesser (Bezugsdurchmesser oder effektiver Durchmesser) [m] |
|
D e |
Effektiver Riemenscheibendurchmesser (außen) [m] |
|
h w |
Nennhöhe (für effektives System h w = 0) [m] |
|
a |
Teillinienversatz (im effektiven System negativ) [m] |
|
D |
Nenndurchmesser und Außendurchmesser für flache Riemenscheibe [m] |
|
h |
Riemenhöhe [m] |
|
D d |
Bezugsdurchmesser der Riemenscheibe [m] |
|
C |
Achsabstand [m] |
| β |
Umspannungswinkel [°] |
|
L d |
Bezugslänge der Riemenscheibe [m] |