Ermüdungskurven in Schweißverbindungen

Zur Bestimmung der Ermüdungsfestigkeit von Schweißverbindungen können unterschiedliche Typen von Ermüdungskurven verwendet werden. Im Folgenden sind Formeln für einzelne Kurven bei Normal- und Scherspannung aufgeführt.

1. Methode der virtuellen Beanspruchung

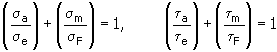
Dabei gilt:

	σ a , τ a	Stärke der Normalspannung (Scherspannung) [MPa, psi]
	σ e , τ e	Ermüdungsgrenze bei konstanter Festigkeit [MPa, psi]
	σ m , τ m	Mittlere Spannung des Zyklus [MPa, psi]
	σ F , τ F	Virtueller Spannungsmittelwert [MPa, psi]
	Ψ	Koeffizient der Haigh-Diagrammverengung [-]
		Ist abhängig vom Material der Verbindung - Empfohlene Werte - für Zug und Biegung Ψ<0.15...0.3>
		- für Schub Ψ <0.1...0.25>

2. Modifizierte Methode nach Godman

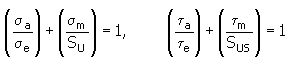
Dabei gilt:

	σ a , τ a	Stärke der Normalspannung (Scherspannung) [MPa, psi]
	σ e , τ e	Ermüdungsgrenze bei konstanter Festigkeit [MPa, psi]
	σ m , τ m	Mittlere Spannung des Zyklus [MPa, psi]
	S U	Zugfestigkeit [MPa, psi]
	S US	Maximale Schubfestigkeit [MPa, psi]
		wobei: S US ≈ 0.8 S U

3. Quadratische (elliptische) Methode

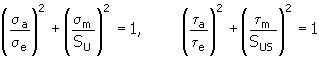
Erläuterung der Variablen unter Punkt 2, modifizierte Methode nach Godman

4. Parabolische Methode nach Gerber

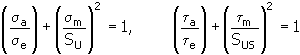
Erläuterung der Variablen unter Punkt 2, modifizierte Methode nach Godman

5. Methode nach Keccecioglu, Chester und Dodge

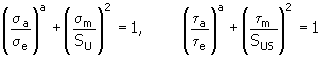
Dabei gilt:

	σ a , τ a	Stärke der Normalspannung (Scherspannung) [MPa, psi]
	σ e , τ e	Ermüdungsgrenze bei konstanter Festigkeit [MPa, psi]
	σ m , τ m	Mittlere Spannung des Zyklus [MPa, psi]
	S U	Zugfestigkeit [MPa, psi]
	S US	Maximale Schubfestigkeit [MPa, psi]
		wobei: S US ≈ 0.8 S U
	a	Exponent, abhängig vom Verbindungsmaterial [-]
		empfohlene Werte <2.6...2.75>

6. Methode nach Bagci

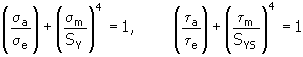
Dabei gilt:

	σ a , τ a	Stärke der Normalspannung (Scherspannung) [MPa, psi]
	σ e , τ e	Ermüdungsgrenze bei konstanter Festigkeit [MPa, psi]
	σ m , τ m	Mittlere Spannung des Zyklus [MPa, psi]
	S Y	Zugelastizitätsgrenze [MPa, psi]
	S YS	Schubelastizitätsgrenze [MPa, psi]
		wobei: S YS ≈ 0.577 S Y

7. Methode nach Soderberg

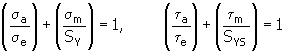
Erläuterung der Variablen unter Punkt 6, Methode nach Bagci