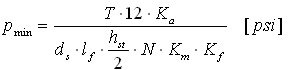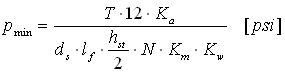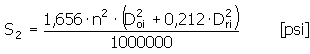Formeln zur Berechnung von Kerbzahnprofilen in englischen Einheiten

Übertragenes Drehmoment

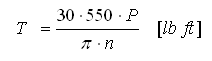
Dabei gilt:

	P	Übertragene Leistung [lb ft]
	n	Drehzahl [min -1 ]

Minimaler Wellendurchmesser

1. Innendurchmesser der Welle d _h > 0

a)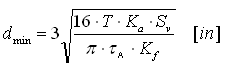

b) wenn d _min ≤d _h -> d _min = 1.1 d _h [in]

c) wenn d _min ≤ 1.5 d _h -> d _min = 1.5 d _h [in]

2. Innendurchmesser der Welle d _h = 0

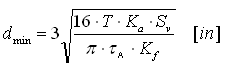
Dabei gilt:

	d min	Minimaler Wellendurchmesser [in]
	d h	Innendurchmesser der Welle [in]
	T	Drehmoment [lb ft]
	K a	Anwendungskoeffizient
	K f	Gebrauchsermüdungskoeffizient
	S v	Angestrebte Sicherheit
	τ Al	Zulässige Scherspannung

Allgemeine Berechnung

Minimale Länge der Kerbverzahnungen zum Übertragen des Drehmoments

1. Feste Verbindung:

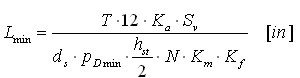
2. Flexible Verbindung:

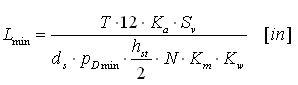
Dabei gilt:

	T	Drehmoment [lb ft]
	K a	Anwendungskoeffizient
	K f	Gebrauchsabnutzungskoeffizient
	K w	Anwendungskoeffizient
	K m	Koeffizient für Lastverteilung
	S v	Angestrebte Sicherheit
	d s	Mittlerer Durchmesser = (D + d) / 2 [in]
	D	Außendurchmesser des Nutquerschnitts [in]
	d	Innendurchmesser des Nutquerschnitts [in]
	N	Anzahl der Nuten [-]
	h	Höhe der Nut = (D - d) / 2 [in]
	s	Fase [in]
	h st	Verbindungshöhe h st = h - 2 s [in]
	p Dmin	Zulässiger Druck auf die tragende Fläche von Welle oder Nut [psi]

Zulässiger Druck

1. Feste Verbindung:
2. Flexible Verbindung:
Dabei gilt:

	T	Drehmoment [lb ft]
	K a	Anwendungskoeffizient
	K f	Gebrauchsabnutzungskoeffizient
	K w	Anwendungskoeffizient
	K m	Koeffizient für Lastverteilung
	S v	Angestrebte Sicherheit
	d s	Mittlerer Durchmesser = (D + d) / 2 [in]
	D	Außendurchmesser des Nutquerschnitts [in]
	d	Innendurchmesser des Nutquerschnitts [in]
	N	Anzahl der Nuten [-]
	h	Höhe der Nut = (D - d) / 2 [in]
	s	Fase
	h st	Verbindungshöhe h st = h - 2 s [in]
	l f	Wirksame Federlänge [in]

Festigkeitskontrolle

p _min ≤ p _Ds

p _min ≤ p _Dh

Dabei gilt:

	p min	Minimaler berechneter Druck h/2 [psi]
	p Ds	Zulässiger Druck in der Welle [psi]
	p Dh	Zulässiger Druck in der Nabe [psi]

Scherspannung im Zahngrund der äußeren Nutung

Bei einem übertragenen Drehmoment T die Scherspannung, die in der Welle unter dem Fußdurchmesser einer Außenkerbverzahnung entsteht

Bei einer Vollwelle

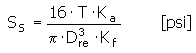
Bei einer Hohlwelle

Anmerkung: Die berechnete Spannung sollte die Werte in der Tabelle nicht überschreiten.

Scherspannung an der Teilungsweite der Nutung

Die Scherspannung an der Teilungsweite der Nutung für ein übertragenes Drehmoment T

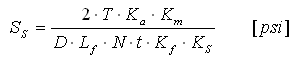
Berechnete Länge der Kerbverzahnung:

L _f = min {L, Le} [in]

Druckspannung an Flanken der Kerbverzahnungszähne

Die zulässige Druckspannung bei Kerbverzahnungen ist wesentlich geringer als bei Zahnradzähnen, da uneinheitliche Belastungsverteilung und Ungleichachsigkeit zu ungleicher Lastenverteilung und Belastung der Zahnspitzen führen.

Bei flexiblen Kerbverzahnungen

Bei festen Kerbverzahnungen

Anmerkung: Die berechnete Spannung sollte die Werte in der Tabelle nicht überschreiten.

Dabei gilt:

Berechnete Länge der Kerbverzahnung	L f = min {L, Le} [in]
Tiefe der Verzahnung h h ≅ 0.9 / P [in]	für Kerbverzahnungen mit flachem Nutboden
h ≅ 1 / P [in]	für Kerbverzahnungen mit abgerundetem Nutboden

Spannung an Festigkeitsgrenze von Kerbverzahnungen

Innenkerbverzahnungen können durch Zugspannung von der radialen Komponente der übertragenen Belastung, Zentrifugalzugspannung oder Zugspannung durch Tangentialkraft an der Teilungsweite der Nutung brechen. Dies führt zu verbogenen Zähnen.

1. Radialzugspannung - Belastung

Dabei gilt: Hülle der Innenkerbverzahnung	t w = D oi - D ri [in]
2. Zentrifugalzugspannung
3. Spannung infolge der Tangenzkräfte

Dabei gilt: Berechnete Länge der Kerbverzahnung

L f = min {L, L e } [in]

4. Die Gesamtzugspannung, bei der der Kranz des externen Glieds zu zerbrechen droht

Anmerkung: Die berechnete Spannung sollte die Werte in der Tabelle nicht überschreiten.

Kronenkerbverzahnungen bei starker Ungleichachsigkeit

Kronenkerbverzahnungen können eine Ungleichachsigkeit von bis zu 5 Grad ausgleichen. Kronenkerbverzahnungen sind erheblich weniger tragfähig als direkte Kerbverzahnungen derselben Größe, wenn die Achsen genau gleich ausgerichtet sind. Bei starker Ungleichachsigkeit ist eine Kronenkerbverzahnung allerdings tragfähiger.

Zahnformen nach ANSI können für externe Glieder einer Kronenkerbverzahnung verwendet werden, sodass sie mit direkten internen Gliedern im Standardformat gepaart werden können.

Druckspannung an den Zähnen

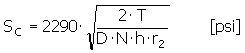
Dabei gilt:

Krümmungsradius des Kronenzahns	r 2 ≅ F 2 / 8 A [in]
Abrundungsradius	r 1 = r 2 tan Φ [in]
Tiefe der Verzahnung h h ≅ 0.9 / P [in]	für Kerbverzahnungen mit flachem Nutboden
h ≅ 1 / P [in]	für Kerbverzahnungen mit abgerundetem Nutboden

Bedeutung der verwendeten Variablen

T	Übertragenes Drehmoment [lb ft]
n	Drehzahl [min -1 ]
D	Teilkreisdurchmesser [in]
D ri	Fußdurchmesser der Innenkerbverzahlung [in]
D re	Fußdurchmesser der Außenkerbverzahnung [in]
D h	Innendurchmesser einer Hohlwelle [in]
D oi	Außendurchmesser der gekerbten Nabe [in]
N	Anzahl der Nuten [-]
h	Höhe der Nut [in]
L f	Berechnete Länge der Kerbverzahnung [in]
L	Aktive Länge Kerbverzahnung [in]
L e	Maximale effektive Länge [in]
t	Effektive Umfangszahndicke [in]
t w	Hülle der Innenkerbverzahnung = Außendurchmesser der Spline-Muffe minus Fußdurchmesser, Differenz geteilt durch 2 [in]
Φ	Schwingwinkel [°]
Y	Der Lewis-Formkoeffizient wird aus der Zahnanordnung abgeleitet. In der Berechnung wird der Wert Y = 1.5 verwendet.
F	Eingriffswinkel [°]
S v	Angestrebte Sicherheit
A	Freistellung der Abrundung an den Zahnenden [in]
r 1	Rundungsradius der Kronenkerbverzahnung [in]
r 2	Krümmungsradius der abgerundeten Zähne für die Kronenkerbverzahnung [in]
K a	Anwendungskoeffizient
K f	Gebrauchsabnutzungskoeffizient
K w	Anwendungskoeffizient
K m	Koeffizient für Lastverteilung
K s	Koeffizient für zahnseitigen Kontakt
	K s = 0.5 für Kerbverzahnungen mit normaler und höherer Lagerungsgenauigkeit (die Belastung wird nur von der Hälfte der Zähne übertragen)
	K s = 0.3 für Kerbverzahnungen mit geringerer Produktions- und Montagegenauigkeit (die Belastung wird nur von einem Drittel der Zähne übertragen)