Dieses Programm erstellt eine vorläufige Konstruktion für das Lagerspiel des Zapfendurchmessers und die Drehzahl des angegebenen Lagers. Der Wert für das Lagerspiel wird anhand eines relativen Lagerspiels mithilfe der folgenden empirischen Formel berechnet:
Dabei gilt:
| Ψ |
Relatives Spiel [-] |
|
|
v H |
Umfangsgeschwindigkeit des Zapfens [m s -l ] |
Das relative Lagerspiel ist ein wichtiger Konstruktionsparameter, welcher sich auf die Lagereigenschaften auswirkt. Der Bereich liegt in der Regel zwischen 0.0005 und 0.004. Kleine Werte für das relative Lagerspiel eignen sich für Lager mit einem hohen spezifischen Druck und geringer Gleitgeschwindigkeit sowie umgekehrt.
Je höher das relative Lagerspiel ist, umso niedriger ist die Tragfähigkeit des Lagers. Hierdurch erhöht sich das Risiko der Zapfenvibration und der Kavitation der Lagerauskleidung. Die Geschwindigkeit des Gleitzapfens wirkt sich maßgeblich auf die Auswahl des radialen Lagerspiels aus. Diese Auswahl basiert auf dem Auskleidungsmaterial und dem Verwendungszweck:
|
Babbitt-Metall |
(0.5 ~ 1) .10 -3 |
|
Bronze |
(0.8 ~ 2) .10 -3 |
|
Aluminiumlegierungen |
(1.2 ~ 2.5) .10 -3 |
|
Gusseisen, Graphit |
(2 ~ 3) .10 -3 |
|
Kunststoffe |
(1.5 ~ 10) .10 -3 |
Für schmale und präzise Lager werden niedrigere Werte ausgewählt, da keine Kantenbelastung auftritt.
Reduzierung des Innendurchmessers der Buchse, da diese in das Lagergehäuse gepresst wird:
Die Buchse wird in das Lagergehäuse mit relativen Überstand gepresst:
Dabei entsteht etwas Kontaktdruck:
Dabei gilt:
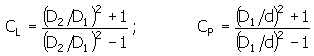 |
Empfohlene Größe des relativen Überstands:
ϑ ≈ 1.3. 10 -3 - Lagergehäuse aus Aluminiumlegierung;
ϑ ≈ 0.6. 10 -3 - Lagergehäuse aus Gusseisen oder Stahl.
Die Änderung des Lagerspiels durch das Einpressen der Buchse wird mithilfe der folgenden Gleichung berechnet:
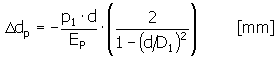
Änderung des Lagerspiels durch den radialen Temperaturgradienten:
Die Lagerbauteile dehnen sich aufgrund der während des Betriebs zunehmenden Temperatur aus. Durch den radialen Temperaturgradienten ändert sich das radiale Lagerspiel in folgendem Maße:
Δ φ T = (α L - α H ) (1 - B) (T V - T U ) - 0.6 (α L ΔT rL - 0.75 α H Δ T rH
Dabei gilt:
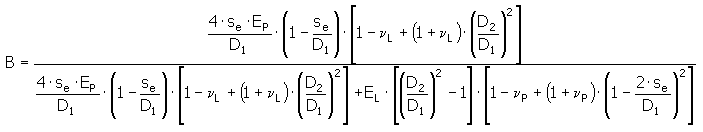 |
Die effektive Stärke der Buchse ist: s e = (D1 - d s V ) / 2 [mm]
Der radiale Temperaturgradient zwischen der äußeren Lageroberfläche und der Gleitfläche beträgt:
ΔT rL ≈ 5 ... 15 [°C]
Der radiale Temperaturgradient zwischen der Gleitfläche und der Wellenmitte beträgt:
ΔT rH 11.0pt ≈ 2 ... 5 [°C]
Die Änderung des Lagerspiels durch den radialen Temperaturgradienten wird mithilfe der folgenden Gleichung berechnet:
Δd T =Δφ T d [mm]
Bedeutung der verwendeten Variablen:
|
d |
Zapfendurchmesser [mm]. |
|
D 1 |
Innerer Lagerdurchmesser [mm]. |
|
D 2 |
Äußerer Lagerdurchmesser [mm]. |
|
Δd p |
Änderung des Lagerspiels durch Klemmung der Buchse infolge von Druck [mm]. |
|
ΔdT |
Änderung des Lagerspiels durch den radialen Temperaturgradienten [mm]. |
|
Δd 1 |
Mittelwert für die Abweichungen infolge des Einpressens der Buchse in den Lagerkörper [μm]. |
|
E L |
Elastizitätsmodul des Lagermaterials [Mpa]. |
|
E p |
Elastizitätsmodul des Buchsenmaterials [Mpa]. |
|
S e |
Effektive Dicke der Buchse [mm]. |
|
S v |
Dicke der Buchsenauskleidung [mm]. |
|
T U |
Temperatur in der näheren Umgebung des Lagers [°C]. |
|
T v |
Mittlere Temperatur des Schmiermittels am Lageraustritt [°C]. |
|
ΔT |
Radialer Temperaturabfall zwischen der äußeren Lageroberfläche und der Gleitfläche [°C]. |
|
ΔT rH |
Radialer Temperaturabfall zwischen der äußeren Lageroberfläche und der Gleitfläche [°C]. |
|
ΔT rL |
Radialer Temperaturabfall zwischen der Gleitfläche und der Wellenmitte [°C]. |
|
α L |
Koeffizient für die Wärmeausdehnung des Lagerkörpers [°C -l ]. |
|
α H |
Koeffizient für die Wärmeausdehnung des Lagerzapfenmaterials [°C -l ]. |
|
ν L |
Poissonsche Konstante für das Lagerkörpermaterial [-]. |
|
ν p |
Poissonsche Konstante für das Buchsenmaterial [-]. |
| υ |
Relativer Überstand [-]. |