Allgemeine Berechnungsformeln
Gebrauchskoeffizient des Materials
Außendurchmesser der Feder
D 1 = D + d [mm]
Dabei gilt:
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
|
d |
Drahtdurchmesser [mm] |
Innendurchmesser der Feder
D 2 = D - d [mm]
Dabei gilt:
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
|
d |
Drahtdurchmesser [mm] |
Arbeitshub
H = L 8 - L 1 = s 8 - s 1 [mm]
Dabei gilt:
|
L 8 |
Länge der voll belasteten Feder [mm] |
|
|
L 1 |
Länge der Feder bei minimaler Arbeitskraft [mm] |
|
|
s 8 |
Verformung der voll belasteten Feder [mm] |
|
|
s 1 |
Verformung der Feder bei minimaler Arbeitskraft [mm] |
Höhe der Federöse
![]()
Dabei gilt:
|
L 0 |
Länge der Feder in unbelastetem Zustand [mm] |
|
|
L Z |
Länge des Federkörpers [mm] |
Federindex
c = D/d [-]
Dabei gilt:
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
|
d |
Drahtdurchmesser [mm] |
Korrekturkoeffizient nach Wahl
![]()
Dabei gilt:
|
c |
Wickelverhältnis [-] |
|
|
L Z |
Länge des Federkörpers [mm] |
Vorspannkraft
![]()
Dabei gilt:
|
d |
Drahtdurchmesser [mm] |
|
|
τ 0 |
Spannung im unbelasteten Zustand [MPa] |
|
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
|
K w |
Korrekturkoeffizient der Scherspannung [-] |
Allgemeine Kraft, entwickelt durch die Feder
![]()
Dabei gilt:
|
d |
Drahtdurchmesser [mm] |
|
| τ |
Torsionsspannung ist Kraft pro Einheit. von Federmaterial im Allgemeinen [MPa] |
|
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
|
K w |
Korrekturkoeffizient der Scherspannung [-] |
|
|
G |
Elastizitätsmodul des Federmaterials [MPa] |
Federrate
![]()
Dabei gilt:
|
d |
Drahtdurchmesser [mm] |
|
|
G |
Elastizitätsmodul des Federmaterials [MPa] |
|
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
|
n |
Anzahl der aktiven Windungen [-] |
|
|
F 8 |
Arbeitskraft in der voll belasteten Feder [MPa] |
|
|
F 1 |
Arbeitskraft der minimal belasteten Feder [MPa] |
|
|
H |
Arbeitshub [mm] |
Federentwurfsberechnung
Während des Entwurfs der Feder werden der Drahtdurchmesser, die Anzahl der Windungen und die Länge L 0 der Feder im unbelasteten Zustand für eine vorgegebene Belastung, ein vorgegebenes Material und vorgegebene Einbaumaße festgelegt.
![]()
Falls die berechnete Feder mit keinem Drahtdurchmesser für die Belastung τ 0 entsprechend der Formel übereinstimmt, wird die Federberechnung mit dem korrigierten Belastungswert im unbelasteten Zustand innerhalb des empfohlenen Bereichs erneut durchgeführt.
![]()
Die Feder ohne Vorspannung wird für eine mittlere empfohlene Steigung von t = 0.35 D [mm] entworfen.
Wenn die berechnete Feder mit keinem Drahtdurchmesser der ausgewählten Steigung übereinstimmt, wird die Federberechnung mit dem korrigierten Steigungswert innerhalb des empfohlenen Bereichs 0.3 D ≤ t ≤ 0.4 D [mm] erneut durchgeführt.
Die Federkonstruktion basiert auf der Festigkeitsbedingung τ 8 ≤ u s τ A und den empfohlenen Bereichen einiger geometrischer Federeinbaumaße: L 0 ≤ D und L 0 ≤ 31.5 Zoll und 4 ≤ D/d ≤ 16 und n ≥ 2.
Vorgegebene Belastung, Material und Einbaumaße der Feder
Zuerst werden die Eingabewerte für die Berechnung überprüft und berechnet.
Anschließend wird die Länge der Feder im unbelasteten Zustand berechnet.
![]()
Nach der Berechnung werden der Drahtdurchmesser, die Anzahl der Windungen und die Federdurchmesser entworfen, sodass die Höhe der Hängeöse dem ausgewählten Ösentyp entspricht. Die zuvor erwähnten Bedingungen für die Festigkeit und Geometrie der Feder müssen ebenfalls erfüllt werden. Der Entwurf der Feder muss jedem Federdurchmesserwert entsprechen, der in der Spezifikation angegeben wurde. Falls dies nicht der Fall ist, werden die Begrenzungen des Federdurchmessers durch die Bedingungen für die geometrischen Maße für den minimal und maximal zulässigen Drahtdurchmesser bestimmt.
Alle Federdrahtdurchmesser, die den Bedingungen für die Festigkeit und die geometrischen Maße entsprechen, werden in der Reihenfolge vom kleinsten zum größten berechnet. Die Höhe der Hängeöse und die Anzahl der Windungen werden überprüft. Wenn alle Bedingungen erfüllt sind, wird der Entwurf mit den ausgewählten Werten fertig gestellt, ohne dass andere geeignete Federdrahtdurchmesser berücksichtigt werden, und die Feder wird mit dem geringsten Drahtdurchmesser und der geringsten Windungsanzahl entworfen.
Die berechnete Höhe der Hängeöse muss innerhalb des Bereichs d ≤ o ≤ 30 d liegen. Die Berechnung einer Kombination aus Drahtdurchmesser, Windungsanzahl und Federdurchmesser muss eine Hängeöse ergeben, deren Höhe der Höhe eines Ösengrundtyps entspricht. Der Ösengrundtyp wird durch eine Untersuchung der ganzen deutschen Öse, der englischen Öse und anderer Ösentypen ausgewählt.
Vorgegebene Belastung, Material und Federdurchmesser
Zuerst werden die Eingabewerte für die Berechnung überprüft.
Nach der Prüfung werden der Drahtdurchmesser, die Anzahl der Windungen, die Länge der Feder im unbelasteten Zustand und die Einbaumaße entworfen, sodass die Höhe der Hängeöse dem ausgewählten Ösentyp entspricht. Die oben erwähnten Bedingungen für die Festigkeit und Geometrie der Feder müssen ebenfalls erfüllt werden. Falls die Einbaumaße L 1 oder L 8 in der Spezifikation angegeben sind oder der Federweg der Feder im Betrieb begrenzt ist, muss die Federkonstruktion diese Bedingung erfüllen. Anderenfalls werden die Begrenzungen der Einbaumaße und die Länge der Feder im unbelasteten Zustand durch die oben erwähnten Bedingungen für die geometrischen Maße für den vorgegebenen Federdurchmesser und den minimal oder maximal zulässigen Drahtdurchmesser bestimmt.
Formel für das Entwerfen einer Feder mit einem vorgegebenen Drahtdurchmesser
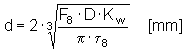
wobei der Wert τ 8 = 0.85 τ A für den Torsionsspannungswert des Federmaterials im voll belasteten Zustand der Feder verwendet wird.
Wenn keine geeignete Kombination aus Federmaßen für diesen Drahtdurchmesser entworfen werden kann, werden alle geeigneten Federdrahtdurchmesser auf ihre geometrischen Maße hin untersucht. Sie werden in der Reihenfolge vom kleinsten zum größten Durchmesser auf Windungsanzahlen hin überprüft, die die den Bedingungen entsprechende Ösenhöhe ergeben. Der Entwurf wird mit den ausgewählten Werten fertig gestellt, ohne dass andere geeignete Federdrahtdurchmesser berücksichtigt werden, und die Feder wird mit dem geringsten Drahtdurchmesser und der geringsten Windungsanzahl entworfen.
Die berechnete Höhe der Hängeöse muss innerhalb des Bereichs d ≤ o ≤ 30 d liegen. Der entsprechende Ösentyp wird für die Ösenhöhe ausgewählt, die auf diese Weise berechnet wird. Die Berechnung einer Kombination aus Drahtdurchmesser, Windungsanzahl, Länge der Feder im unbelasteten Zustand und Einbaumaßen muss eine Hängeöse ergeben, deren Höhe der Höhe eines Ösengrundtyps entspricht. Der Ösengrundtyp wird durch eine Untersuchung der ganzen deutschen Öse, der englischen Öse und anderer Ösentypen ausgewählt.
Vorgegebene maximale Arbeitskraft, Material, Einbaumaße und Federdurchmesser
Zuerst werden die Eingabewerte für die Berechnung überprüft und berechnet.
Anschließend werden der Drahtdurchmesser, die Anzahl der Windungen, die freie Länge der Feder sowie die minimale Arbeitskraft F 1 so konstruiert, dass die Höhe der Hängeöse dem ausgewählten Ösentyp entspricht. Die oben erwähnten Bedingungen für die Festigkeit und Geometrie der Feder müssen ebenfalls erfüllt werden.
Formel für das Entwerfen einer Feder mit einem vorgegebenen Drahtdurchmesser
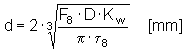
wobei der Wert τ 8 = 0.9 τ A für den Torsionsspannungswert des Federmaterials im voll belasteten Zustand der Feder verwendet wird.
Wenn keine geeignete Kombination aus Federmaßen für diesen Drahtdurchmesser entworfen werden kann, werden alle geeigneten Federdrahtdurchmesser auf ihre geometrischen Maße hin untersucht. Sie werden in der Reihenfolge vom kleinsten zum größten Durchmesser auf Windungsanzahlen hin überprüft, die die den Bedingungen entsprechende Ösenhöhe ergeben. Der Entwurf wird mit den ausgewählten Werten fertig gestellt, ohne dass andere geeignete Federdrahtdurchmesser berücksichtigt werden, und die Feder wird mit dem geringsten Drahtdurchmesser und der geringsten Windungsanzahl entworfen.
Kontrollberechnung der Feder
In der Kontrolle werden entsprechende Werte der Einbaumaße und des Arbeitshubs für die vorgegebene Belastung, das vorgegebene Material und die Federmaße berechnet.
Zuerst werden die Eingabewerte für die Berechnung überprüft. Dann werden die Einbaumaße mithilfe der folgenden Formeln berechnet.
Länge der vorbelasteten Feder
![]()
Länge der voll belasteten Feder
![]()
Dabei gilt:
|
L 0 |
Länge der Feder in unbelastetem Zustand [mm] |
|
|
F 1 |
Arbeitskraft der minimal belasteten Feder [mm] |
|
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
|
n |
Anzahl der aktiven Windungen [-] |
|
|
G |
Elastizitätsmodul des Federmaterials [MPa] |
|
|
d |
Drahtdurchmesser [mm] |
|
|
F 8 |
Arbeitskraft in der voll belasteten Feder [MPa] |
Arbeitshub
H = L 1 - L 8 [mm]
Berechnung der Arbeitskräfte
Die entsprechenden Kräfte, die die Feder im jeweiligen Arbeitszustand erzeugt, werden für das vorgegebene Material, die vorgegebenen Einbaumaße und die vorgegebenen Federmaße berechnet. Zuerst werden die Eingabewerte überprüft und berechnet, dann werden die Arbeitskräfte mithilfe der folgenden Formeln berechnet.
Minimale Arbeitskraft
![]()
Maximale Arbeitskraft
![]()
Berechnung der Federausgangsparameter
Diese sind für alle Federberechnungstypen gleich und werden in folgender Reihenfolge berechnet:
Koeffizient für Ösenhöhe
![]()
Federrate
![]()
Länge des Federkörpers
|
Feder ohne Vorspannung |
|
|
L z = t n + d [mm] |
|
|
Feder mit Vorspannung |
|
|
L z = 1.03 (n + 1) d [mm] |
|
Verformung bei minimaler Arbeitskraft
s 1 = L 1 - L 0 [mm]
Verformung im voll belasteten Zustand
s 8 = L 8 - L 0 [mm]
Torsionsspannung des Federmaterials im vorbelasteten Zustand
![]()
Torsionsspannung des Federmaterials bei voll belasteter Spannung
![]()
Kraft im Grenzzustand
![]()
Verformung im Grenzzustand
![]()
Dabei gilt:
|
k |
Federrate [N/mm] |
|
|
F 9 |
Arbeitskraft einer im Grenzzustand belasteten Feder [N] |
|
|
F 0 |
Vorspannkraft der Feder [N] |
Länge der Feder im Grenzzustand
L 9 = L 0 + s 9 [mm]
Verformungsenergie der Feder
![]()
Abgewickelte Drahtlänge
|
l = 3.2 D n + l 0 [mm] |
|||
|
Mit abgewickelter Ösenlänge l 0 : |
|||
|
Halbe deutsche Öse |
|||
|
π - 2 d [ |
|||
|
Ganze deutsche Öse |
|||
|
l 0 = 2 (π D - 2 d) [mm] |
|||
|
Ganze deutsche Öse seitlich hochgestellt |
|||
|
l 0 = 2 (π D - 2 d) [mm] |
|||
|
Englische Öse |
|||
|
l 0 = 2 (π D - d) [mm] |
|||
|
Hakenöse |
|||
|
l 0 = π D + 2 o - D + 3 d [mm] |
|||
|
Doppelte deutsche Öse |
|||
|
l 0 = 4 π D [mm] |
|||
|
Doppelte deutsche Öse seitlich hochgestellt |
|||
|
l 0 = 4 π D [mm] |
|||
|
Alle anderen Ösentypen |
|||
|
l 0 = 0 [mm] |
|||
Federgewicht
![]()
Eigenfrequenz der Feder
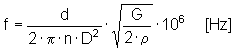
Kontrolle der Federbelastung
τ 8 ≤ u s τ A
Übersicht über die verwendeten Variablen:
|
d |
Drahtdurchmesser [mm] |
|
k |
Federrate [N/mm] |
|
D |
Mittlerer Durchmesser der Feder [mm] |
|
D 1 |
Außendurchmesser der Feder [mm] |
|
D 2 |
Innendurchmesser der Feder [mm] |
|
F |
Allgemeine Kraft, entwickelt durch die Feder [N] |
|
G |
Schubmodul des Federmaterials [MPa] |
|
H |
Arbeitshub [mm] |
|
c |
Wickelverhältnis [-] |
|
K w |
Korrekturkoeffizient der Scherspannung [-] |
|
l |
Abgewickelte Drahtlänge [mm] |
|
L |
Allgemeine Federlänge [mm] |
|
L Z |
Länge des Federkörpers [mm] |
|
m |
Federgewicht [N] |
|
n |
Anzahl der aktiven Windungen [-] |
|
o |
Höhe der Hängeöse [mm] |
|
t |
Steigung der aktiven Windungen bei unbelasteter Feder [mm] |
|
s |
Allgemeiner Federweg (Ausdehnung) [mm] |
|
u s |
|
| ρ |
Dichte des Federmaterials [N/mm 3 ] |
| τ |
Torsionsspannung ist Kraft pro Einheit. von Federmaterial im Allgemeinen [MPa] |
|
τ A |
Zulässige Torsionsspannung des Federmaterials [MPa] |