Grundlegende Tellerfederberechnung

Die Berechnung erfolgt in metrischen oder Zoll-Einheiten. Bei Auswahl der ANSI-Norm erfolgt die Berechnung in Zoll-Einheiten.

Die Berechnung erfolgt auf der XY- und der XZ-Ebene; hiervon wird die quadratische Summe gebildet.

Berechnete Parameter

Freie Höhe der stumpfen Spitze einer freien Feder

h = H - t [mm, in]

Dabei gilt:

	H	Freie Höhe der Feder [mm, in]
	t	Stärke des Federmaterials [mm, in]

Durchmesserverhältnis

Dabei gilt:

	D	Außendurchmesser der Feder [mm, in]
	d	Innendurchmesser der Feder [mm, in]

Berechnungsfaktor α

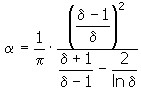
Berechnungsfaktor β

Berechnungsfaktor γ

Zulässiger Federweg des Einzeltellers

s _m = h [mm, in]

Dabei gilt:

h

Freie Höhe der stumpfen Spitze einer Feder [mm, in]

Kraft bei maximalem Federweg (im Grenzzustand)

Dabei gilt:

	E	Elastizitätsmodul der Feder [MPa, psi]
	t	Stärke des Federmaterials [mm, in]
	s m	Verformung im Grenzzustand [mm, in]
	μ	Poissonsche Konstante [-]
	α	Berechnungsfaktor [-]
	D	Außendurchmesser der Feder [mm, in]

Von der Feder beim Weg s ausgeübte Kraft

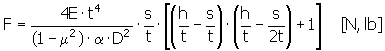
Dabei gilt:

	E	Elastizitätsmodul der Feder [MPa, psi]
	t	Stärke des Federmaterials [mm, in]
	s	Arbeitshub der Feder [mm, in]
	μ	Poissonsche Konstante [-]
	α	Berechnungsfaktor [-]
	D	Außendurchmesser der Feder [mm, in]
	h	Freie Höhe der stumpfen Spitze einer Feder [mm, in]

Maximale Druckspannung in der Feder beim Weg s

Dabei gilt:

	E	Elastizitätsmodul der Feder [MPa, psi]
	t	Stärke des Federmaterials [mm, in]
	s	Arbeitshub der Feder [mm, in]
	μ	Poissonsche Konstante [-]
	α	Berechnungsfaktor [-]
	D	Außendurchmesser der Feder [mm, in]
	h	Freie Höhe der stumpfen Spitze einer Feder [mm, in]
	γ	Berechnungsfaktor [-]

Gesamtzahl der Federn in einem Satz

χ = n i [-]

Dabei gilt:

	n	Anzahl der Federn in einem Satz mit paralleler Anordnung [-]
	i	Anzahl der Federn in einem Satz mit gegenüberliegender Anordnung oder Anzahl der Sätze mit paralleler Anordnung in einem Satz mit kombinierter Anordnung [-]

Hub (Durchbiegung) des Federsatzes

z = i s [mm, in]

Dabei gilt:

	i	Anzahl der Federn in einem Satz mit gegenüberliegender Anordnung oder Anzahl der Sätze mit paralleler Anordnung in einem Satz mit kombinierter Anordnung [-]
	s	Arbeitshub der Feder [mm, in]

Von einem Federsatz ausgeübte Kraft

F = n F ₁ [N, lb]

Dabei gilt:

	n	Anzahl der Federn in einem Satz mit paralleler Anordnung [-]
	F 1	Von einer Unterlegscheibe ausgeübte Kraft [N, lb]

Länge der Feder im nicht belasteten Zustand

L ₀ = i (h + n t ) [mm, Zoll]

Dabei gilt:

	h	Freie Höhe der stumpfen Spitze einer Feder [mm, in]
	i	Anzahl der Federn in einem Satz mit gegenüberliegender Anordnung oder Anzahl der Sätze mit paralleler Anordnung in einem Satz mit kombinierter Anordnung [-]
	n	Anzahl der Federn in einem Satz mit paralleler Anordnung [-]
	t	Stärke des Federmaterials [mm, in]

Länge des belasteten Federsatzes

L = L ₀ - z [mm, Zoll]

Dabei gilt:

	L 0	Länge der Feder im nicht belasteten Zustand [mm, in]
	z	Hub (Verschiebung) des Federsatzes [mm, in]

Bedeutung der verwendeten Variablen

d	Innendurchmesser der Feder [mm, in]
D	Außendurchmesser der Feder [mm, in]
F 1	Von einer Unterlegscheibe ausgeübte Kraft [N, lb]
E	Elastizitätsmodul der Feder [MPa, psi]
t	Stärke des Federmaterials [mm, in]
s	Arbeitshub der Feder [mm, in]
μ	Poissonsche Konstante [-]
i	Anzahl der Federn in einem Satz mit gegenüberliegender Anordnung oder Anzahl der Sätze mit paralleler Anordnung in einem Satz mit kombinierter Anordnung [-]
n	Anzahl der Federn in einem Satz mit paralleler Anordnung [-]
H	Freie Höhe der Feder [mm, in]