Footfall analysis examines the effect of human footfall loading (interpreted as a harmonic force in a certain frequency interval) on structure vibrations.
The Footfall analysis applies only to structures without material, geometrical and structural non-linearities. If a structure includes elasto-plastic bars, non-linear or unidirectional supports, releases, compatibilities, cables and compression / tension elements, you cannot define the Footfall analysis.
The aim of the analysis is to evaluate a vertical response (response factor, acceleration, velocity, displacement) in the structure nodes, that is induced by the harmonic force applied to the nodes. The harmonic force varies in the fixed frequency range (FRF).
There are 2 approaches to analyzing the footfall effects:
- analyze the response in the same node to which the force is applied (self excitation)
- analyze the response in any node to the effect of the force applied to another node (full excitation).
A harmonic force is applied to each of selected structure nodes using the FRF analysis mechanism considering damping. You can define the frequency domain for the harmonic force (the default frequency range changes depending on the selected excitation method). The frequency domain is divided to 20 intervals considering additional points for the frequency of eigenvibrations.
Results of the analysis include only results in nodes. One of the most important results of the analysis is a response factor which specifies how many times calculated vibrations exceed the allowable ones, perceptible to a human.
After the analysis, you can display results in nodes as:
- node table (to access it, select Results menu > Advanced > Footfall Analysis - Tables option)
- maps on panels and bars (to access it, select Results menu > Advanced > Footfall Analysis - Maps option)
- diagrams (to access it, select Results menu > Advanced > Footfall Analysis - Diagrams option).
You can calculate the response factor using 2 different types of analysis:
- resonant response analysis
- impulsive, transient response analysis.
The criterion of selecting an analysis type is the first, basic frequency of structure eigenvibrations and the maximum footfall frequency.
Excitation forces according toConcrete Centre (2006)
Resonant response analysis
The resonant response analysis consists in distributing the function of vibrations into Fourier series which has harmonic components. Up to 4 components of the series are used. The 4-fold maximum value of the interval of the footfall frequency is usually approx. 8-10 Hz. If a basic frequency of eigenvibrations is less than this value, resonant vibrations can build up in the interval of excitation. Calculate the acceleration for each of the 4 harmonic components at each step of the interval of excitation frequency. Next, calculate a response factor for each of the harmonic components by comparing the calculated acceleration with the base acceleration aR=1 (m/s2):
for f h < 4 Hz
for 4 Hz < fh < 8 Hz
a R=1,h = 0.0071
for f h > 8 Hz
The response factor for the harmonic component h:
Calculate the overall response factor for the resonant response analysis as a square root of the sum of squares of 4 response factors for the harmonic components.
Transient response analysis
If a structure is more rigid, with the basic frequency of eigenvibrations over 10 Hz, resonant vibrations do not build up. Each of the walker's footstep induces vibrations by a single excitation fading in time. Perform only the transient response analysis for a single impulse induced for the maximum value of the footfall frequency. A result of the analysis is a plot of the velocity function in time. A measure of vibrations is a mean value of the transient velocity function, that is root mean square velocity:
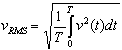
Calculate a response factor for the transient response analysis as:
Rf = v RMS / vR=1
where basic velocity v R=1 (m/s) is:
v R=1 = 5.0 * 10-3 / 2 π f1 for the basic vibration frequency f 1 < 8 Hz
v R=1 = 1.0 * 10 -4 for f 1 ≥ 8 Hz.
A structure with the basic eigenvibration frequency of approx. 8-10 Hz can be influenced by resonant and impulse vibrations. The software performs both vibration analyses and specifies the total vibration coefficient as the greater of the coefficients from both types of analysis.
Excitation forces according toSCI P354:Design of Floors for Vibration
The response factor for the resonant and transient analyses is calculated based on the mean acceleration RMS that is weighted by the a w,rms frequency.
The response factor is calculated as:
R f = a RMS / aR=1
where the base acceleration aR=1 (m/s2), for vertical vibrations, with respect to the Z axis, according to BS 6472 and ISO 10137, equals:
a R=1 = 5*10-3
Excitation forces according to AISC DG11: Floor Vibrations due to Human Activity
The analysis is carried out only for the condition of permanent, resonant vibrations. There are no results for non-permanent vibrations in this method.
The response factor is calculated on the base of maximum acceleration with respect to the gravitational acceleration g.
R f = a p / g
The allowable acceleration according to AISC DG11 Table 4.1 a 0 / g is:
- for office buildings, apartment buildings and churches 0.005 (0.5 %)
- for trading areas 0.015 (1.5 %).
References:
- A Design Guide for Footfall Induced Vibration of Structures, M.R. Willford, P.Young, The Concrete Center 2006
- SCI P354: Design of Floors for Vibration: A New Approach The Steel Construction Institute (2007 Edition)
- Steel Design Guide Series 11, Floor Vibrations Due to Human Activity, AISC 2003