A concentrated force applied at a point along a bar length acts along the longitudinal bar axis. To easily define loads acting at points that are not positioned on the longitudinal bar axis, you can define a displacement (eccentricity) of the force in relation to the longitudinal bar axis.
Loads defined on eccentricity are reduced to a bar axis.
Load generation for a general 3D case is shown in the following image.
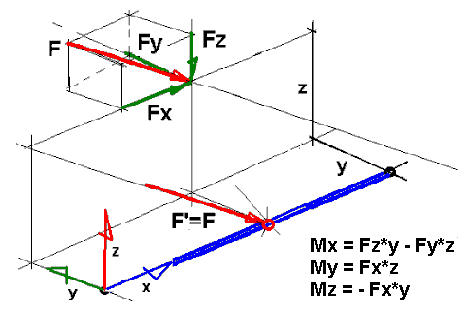
The following applies to loads on eccentricity:
- A concentrated moment defined on an eccentricity does not generate any additional loads.
- A concentrated force defined with a distance to a bar axis is moved to the x
0
application point with the same F force value and direction of action. Also, concentrated moments applied to an x
0
point are generated. Concentrated force components (in relation to the local element coordinate system) Fx, Fy, Fz are found. Next, additional moments in a local system can be calculated.
Mx = Fz*y - Fy*z
My = Fx*z
Mz = - Fx*y
- A uniform load defined on an eccentricity is applied to the whole length with the same p load value and direction of action. Also, a uniform moment load is generated along the whole length of a bar. As for concentrated forces, when uniform load components px, py, and pz are found, a uniform load should be generated:
mx = pz*y - py*z
my = px*z
mz = - px*y.
Note: Depending on the type of structure, the following limits apply:
- For 2D structures (FRAME 2D, TRUSS 2D), an eccentricity is defined only in the z direction. Field y is not accessible in a dialog at that time. As a general rule for 2D structures, loads in a local system are not rotated with a gamma angle. The same rule applies to the eccentricity direction of loads. to Only My moments are generated.
- For 2D structures (PLATE and GRILLAGE) type, an eccentricity is defined in a y and z direction. As a general rule for 2D structures, loads in a local system are not rotated with a gamma angle. The same applies to the eccentricity direction of loads. Only Mx= Fz*y - 0*z moments are generated.