About Splines

A spline is a smooth curve that passes through or near a set of points that influence the shape of the curve.

By default, a spline is a series of blended curve segments of degree 3 (also called cubic) polynomials. These curves are technically called nonuniform rational B-splines (NURBS), but are referred to as splines for simplicity. Cubic splines are the most common, and mimic the splines that are created manually using flexible strips that are shaped by weights at data points.

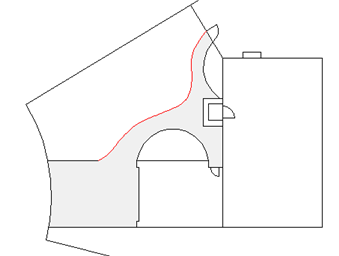
In the following example, a spline was used to create the highlighted boundary of the concrete walkway.

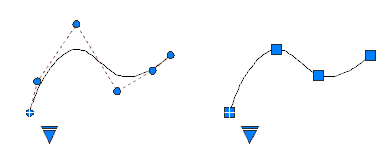
Understand Control Vertices and Fit Points

You can create or edit splines using either control vertices, or fit points. The spline on the left displays control vertices along a control polygon, and the spline on the right displays fit points.

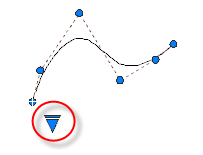
Use the triangular grip on a selected spline to switch between displaying control vertices and displaying fit points. You can use the round and square grips to modify a selected spline.

Important: Switching the display from control vertices to fit points automatically changes the selected spline to degree 3. Splines originally created using higher-degree equations will likely change shape as a result.

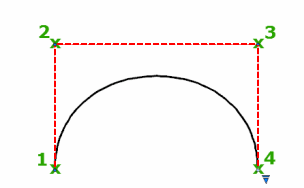
Create Splines Using Control Vertices

When you create splines using control vertices, the points you specify display temporary lines between them, forming a control polygon that determines the shape of the spline.

The advantage of changing the shape of a spline using control vertices is the fine control this method provides. With this method, you can also specify lower or higher degree polynomials, including degree 1 (linear), degree 2 (quadratic), degree 3 (cubic), and so on up to degree 10.

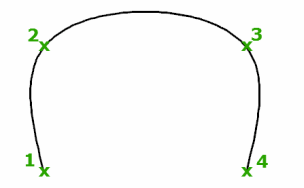
Create Splines Using Fit Points

When you create splines using fit points, the resulting curve passes through the specified points, and is influenced by the spacing of mathematical knots in the curve.

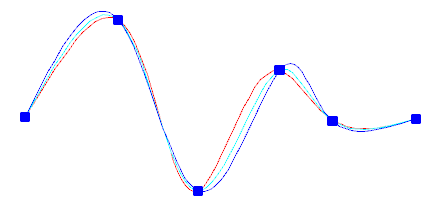
You can choose the spacing of these knots with the knot parameterization option, which will result in different curves as shown in the example.

Note: There is no best choice for knot parameterization for all cases. The chord length parameterization is commonly used, and the square root (centripetal) parameterization often produces better curves depending on the data set.

When the Tolerance value is set to 0, the spline passes directly through the fit points. With larger tolerance values, the spline passes near the fit points. Optionally, you can specify the tangent direction for the spline at each end.

Note: The fit point method always results in a degree 3 spline.

Special Cases

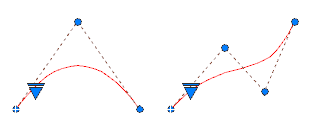
You can create a spline with a parabolic shape by specifying a degree 2 spline created with exactly 3 control vertices as shown on the left. Degree 3 splines created with 4 control vertices have the same shape as Bezier curves of degree 3 as shown on the right.