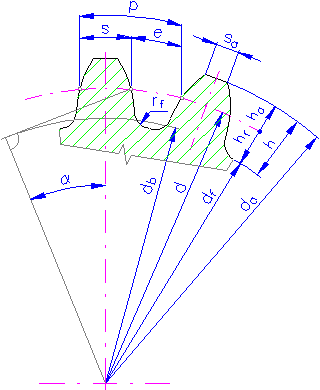
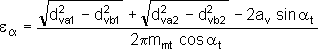Input Parameters
Gear type - according to the position of root and head cone
Gear ratio and tooth numbers ![]()
Pressure angle (the angle of tool profile) α t
Helix angle β m
Axis angle Σ
Tangential module on outer cone met (for metric calculation)
Tangential Diametral Pitch on outer cone Pet (for English units)
Unit addendum height ha *
Unit clearance c *
Unit dedendum fillet r f *
Facewidths b 1 , b 2
Unit correction x = x 1 = - x 2
Unit change of tooth thickness x t = x t1 = - x t2
Auxiliary Geometric Calculations
Distribution of Unit Corrections for Single Gears
Design According to the Strength Calculation
Design of Face Width
Calculation of Maximum Dedendum Filleting
Calculated parameters
|
|
Normal Pressure Angle in Middle Plane
|
tg α nm = tg α t cos β m |
Pitch angle
|
|
Outside pitch diameter
|
d e1,2 = m et z 1,2 |
Outside length of surface line on pitch cone
|
|
Length of surface line on the mean cone
|
R m = R e - 0.5 b |
Relative face width
|
|
Tangential module on the mean cone
|
|
Normal module on the mean cone
|
m mn = m mt cos β m |
Mean pitch diameter
|
d m1,2 = m mt z 1,2 |
Equivalent number of teeth
|
|
Ekvivalent pitch diameter
|
|
Ekvivalent base diameter
|
d vb1,2 = d v1,2 cos α t |
Ekvivalent outside diameter
|
d va1,2 = d v1,2 + 2 h ae1,2 m mt / m et |
Ekvivalent center distance
|
a v = 0.5 (d v1 + d v2 ) |
Virtual gear ratio
|
|
Virtual number of teeth
|
|
Virtual pitch diameter
|
|
Virtual base diameter
|
d bn1,2 = d n1,2 cos α t |
Virtual outside diameter
|
d an1,2 = d n1,2 + 2 h ae1,2 m mt / m et |
Virtual helix angle at the base cylinder
|
sin β b = sin β m cos α nm |
Virtual center distance
|
a n = 0.5 (d n1 + d n2 ) |
Dedendum reduction
|
k 1,2 = 0.02 (17 - z n1,2 ) for k > 0 the dedendum shortening is done |
Addendum
|
h ae1,2 = m et (h a * + x 1,2 - k 1,2 ) |
Dedendum
|
hf e1,2 = m et (h a * + c * - x 1,2 ) |
Outside diameter
|
d ae1,2 = d e1,2 + 2ha e1,2 cos δ 1,2 |
Root diameter
|
d fe1,2 = d e1,2 - 2 hfe1,2 cos δ 1,2 ) |
Outside diameter at small end
|
d ai1,2 = d ae1,2 (1 - φ R ) |
Vertex distance
|
A 1,2 = R e cos δ 1,2 - h ae1,2 sin δ 1,2 |
Outside bevel angle
|
|
Cutting angle
|
|
Tooth thickness (measured normally on the pitch diameter)
|
|
Chordal facewidth (normal)
|
s ke1,2 = s e1,2 cos 2 α t |
Addendum height above the chord
|
|
Unit addendum width (measured normally)
|
|
||
|
where: |
||
|
|
||
Operating width of gears
|
b w = b |
Factor of mesh duration
|
ε = ε + ε
|
Minimum correction without tapering
|
|
||
|
where: |
||
|
h a0 * = h a * + c * - r f * (1 - sin α t ) |
||
Minimum correction without undercut
|
|
Minimum correction without undercut
|
|
Helix angle at end
|
sinβ e = sinβ m R m /R e |
Normal pressure angle at end
|
tanα ne = tanα t cosβe |