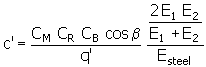Based on the fixed-end beam calculation. Contains the majority of effects.
Safety factors
Contact fatigue

where:
|
σ Hlim |
contact fatigue limit (material property) |
|
|
F t |
tangential force acting at teeth |
|
|
b w |
operating face width |
|
|
d 1 |
pitch diameter of pinion |
Contact during one-time loading
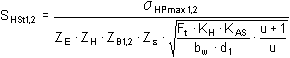
where:
|
σ HPmax |
permissible contact stress |
|
|
K AS |
one-time overloading factor |
Bending fatigue
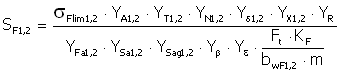
where:
|
σ Flim |
bending fatigue limit (material property) |
|
|
b wF1,2 = min (b 1,2 , b w + 2m) |
tooth width for bending |
Bending during one-time loading
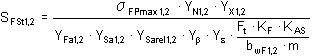
where:
|
σ FPmax |
permissible bending stress |
Factor calculations
Z N ... life factor (for contact)
![]()
1 ≤ Z N ≤ 1.3 nitridated steels
1 ≤ Z N ≤ 1.6 other steels
|
N Hlim |
base number of load cycles for contact (material property) |
|
|
N K1,2 = 60 L h n 1,2 |
required number of load cycles (speed) |
Y N ... life factor (for bending)
![]()
1 ≤ Y N ≤ 1.6 nitridated steels
1 ≤ Y N ≤ 2.5 other steels
|
N Flim |
base number of load cycles for bending (material property) |
|
|
N K1,2 = 60 L h n 1,2 |
required number of load cycles (speed) |
Z L ... lubricant factor
|
DIN and ISO: |
||
|
Z L = C ZL + 4 (1 - C ZL ) 0.158 |
||
|
C ZL = σ Hlim / 4375 + 0.6357 |
||
|
for σ Hlim < 850 Mpa C ZL = 0.83 |
||
|
for σ Hlim > 1200 Mpa C ZL = 0.91 |
||
Z R ... roughness factor
Z V ... speed factor
|
CSN: |
||
|
Z v = 0.95 + 0.08 log v |
||
|
ISO and DIN: |
||
|
C ZV = C ZL + 0.02 |
Z E ... elasticity factor
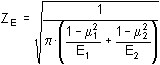
where:
| μ |
Poisson's ratio (material property) |
|
|
E |
modulus of elasticity (material property) |
Z H ... zone factor
![]()
Z B ... single pair tooth contact factor
|
for ε≥ 1 or internal gearing: |
|
|
Z B1,2 = 1 |
|
|
for ε = 0: |
|
|
|
|
|
for ε < 1: |
|
|
Z B1,2 = Z B0 - ε b (Z B0 - 1) where: |
|
|
Z B0 = Z B1,2 calculated for ε = 0 |
|
Z ε ... contact ratio factor
|
for ε = 0: |
|
|
|
|
|
for ε < 1: |
|
|
|
|
|
for ε≥ 1: |
|
|
|
|
Y ... contact ration factor (for bending)
CSN:
|
for ε < 1: |
|
|
|
for ε≥ 1: |
|
ISO and DIN:
|
|
||
Z ... helix angle factor (for contact)
CSN:
|
Z = 1 |
||
ISO and DIN:
|
|
||
Y ... helix angle factor (for bending)
![]()
CSN:
|
Y βmin = 1 - 0.25 ε≥ 0.75 |
ISO and DIN:
|
for ε > 1 the ε = 1 is used |
|
|
for β > 30° the β = 30° is used |
Z x ... size factor (for contact)
Y x ... size factor (for bending)
Z W ... work hardening factor
Y Fa ... form factor

where:
|
h Fa |
bending arm of a force acting on the tooth end |
|
|
s Fn |
thickness of dedendum dangerous section of alternate gear |
|
|
α Fan |
bending angle at the end of straight tooth of alternate gear |
Y Sa ... stress correction factor
Y Sa = (1.2 + 0.13 L a ) q s exp

Y Sag ... teeth with grinding notches factor
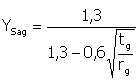

Y ... notch sensitivity factor (depends on the material and curvature radius of dedendum transition)
Y R ... tooth root surface factor
K H ... additional loads factor (for contact)
K H = K A K Hv K Hb K Ha
K F ... additional loads factor (for bending)
K F = K A K Fv K Fb K Fa
K A ... application factor (external dynamic forces)
K Hv ... dynamic factor (internal dynamic forces) for contact
K Fv ... dynamic factor (internal dynamic forces) for bending
![]()
for CSN:
|
at K A F t / b w < 150 considering K A F t / b w = 150 |
for ISO and DIN:
|
at K A F t / b w < 100 considering K A F t / b w = 100 |
|
|
where: K P , K Q ... table values |
K Hβ ... face load factor (for contact)
for CSN:
![]()
where:
|
c = 0.4 |
gears with hardened tooth sides |
|
|
c = 0.3 |
non-hardened gears |
|
|
|
||
|
f ky = | f sh1 + f sh2 | + f kZ - y |
||
|
|
||
|
f b , f x , f y ... teeth tolerance y ... table value |
||
for ISO and DIN:
|
for |
|
|
|
otherwise ( < 1): |
|
|
|
F βy = F βx χ |
||
|
for gears with hardened tooth sides χ = 0.85 |
||
|
for others |
|
|
|
F βx = 1.33 f sh + f ma |
|
q' = 0.04723 + 0.15551/z v1 + 0.25791/z v2 - 0.00635 x 1 - 0.11654 x 1 /z v1 - 0.00193 x 2 - 0.24188 x 2 /z v2 + 0.00529 x 1 2 + 0.00182 x 2 2 |
|
|
|
|
|
for F t K A / b w < 100 the values are interpolated |
|
|
for ISO c' = c' [(F t K A / b w ) / 100] 0.25 |
|
|
for DIN c' = c' (F t K A / b w ) / 100 |
|
|
C M = 0.8 |
|
|
C R = 1 for solid gears |
|
|
C B = [1 + 0.5 (1.2 - h f /m)] [1 - 0.02 (20° - α)] |
|
|
E steel = 206 000 |
|
|
c = c' (0.75 ε + 0.25) |
|
|
|
|
|
A, B ... table values depend on the arrangement of teeth gears, shafts, and bearings |
K Fβ ... face load factor (for bending)
K Fβ = (K Hβ ) NF
where:
|
|
||
|
h = 2 m/ε |
spur gears |
|
|
h = 2 m |
helical gears |
K Fa ... transverse load factor (for bending)
|
for ε < 2: |
|
|
|
|
|
for ε> 2: |
|
|
at K A F t / b w < 100 considering K A F t / b w = 100 |
|
|
|
|
|
limit values: |
|
|
for CSN: 1 ≤ K Fα ≤ε |
|
|
|
K Hα ... transverse load factor (for contact)
|
for CSN: |
|
|
K Hα = 1 for straight teeth |
|
|
K Hα = K Fα for helical teeth |
|
|
DIN and ISO: |
|
|
K Hα = K Fα |
|
|
for limit values: |
|
|
|