Description
Defines material properties for use in elastometric foams.
Format
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| MATHPF | MID | MU1 | ALPHA1 | NU1 | RHO | AV | TREF | GE | |
| NA | |||||||||
| MU2 | ALPHA2 | NU2 | MU3 | ALPHA3 | MU3 | ||||
| MU4 | ALPHA4 | NU4 | MU5 | ALPHA5 | MU5 | ||||
| MU6 | ALPHA6 | NU6 | |||||||
| TAB1 | TAB2 | TAB3 | TABD |
Example
| MATHPF | 100 | 160 | 2 | 0.48 | 0.01 | ||||
| 2 | |||||||||
| 40 | -0.2 | 0 |
| Field | Definition | Type | Default |
|---|---|---|---|
| MID | Material identification number | Integer > 0 | Required |
| MUi | Shear moduli related to distortional deformation. | Real | 0.0, See Remark 2 |
| ALPHAi | Exponents related to distortional deformation. | Real | 0.0, See Remark 2 |
| NUi | Material constants related to volumetric deformation. | Real ≥ 0 | 0.0, See Remark 2 |
| RHO | Mass density in original configuration. | Real | 0.0 |
| AV | Volumetric coefficient of thermal expansion. | Real | 0.0 |
| TREF | Reference temperature for the calculation of thermal loads. | Real | 0.0 |
| GE | Structural element damping coefficient. See Remarks 6 and 8. | Real | 0.0 |
| NA | Order of the strain energy polynomial function. | 0 < Integer ≤ 6 | 1, See Remark 3 |
| TAB1 | Table identification number of TABLES1 entry that contains simple tension/compression data to be used in the estimation of the material constants Aij. xi values in the TABLES1 entry must be stretch ratios
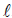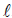 /0 and yi values must be values of the engineering stress
F/A0. Stresses are negative for compression and positive for tension. If this convention is not followed the solution may fail to converge.
|
Integer > 0 or blank | |
| TAB2 | Table identification number of TABLES1 entry that contains equibiaxial tension data to be used in the estimation of the material constants Aij. xi values in the TABLES1 entry must be stretch ratios
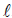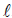/0. yi values must be values of the engineering stress
F/A0.
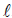is the current length,
F is the current force,
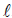0 is the initial length, and
A0 is the cross-sectional area. In the case of pressure of a spherical membrane, the engineering stress is given by
Pr0λ2/2t0 where
P is the current value of the pressure and r0, t0 are the initial radius and thickness.
|
Integer > 0 or blank | |
| TAB3 | Table identification number of TABLES1 entry that contains simple shear data to be used in the estimation of the material constants Aij. xi values in the TABLES1 entry must be values of the shear tangent γ and yi values must be values of the engineering stress F/A0. | Integer > 0 or blank | |
| TABD | Table identification number of TABLES1 entry that contains pure volumetric compression data to be used in the estimation of the material constants Di. xi values in the TABLES1 entry must be values of the volume ratio
J = λ3, where λ =
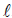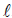/0 is the stretch ratio in all three directions; yi values must be values of the pressure, assumed positive in compression.
|
Integer > 0 or blank |
Remarks
- The hyperfoam generalized strain energy may be expressed as follows:
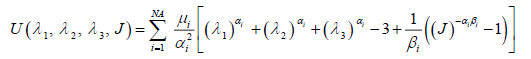
where λ1, λ2, and λ3 are principal stretches; J = detF is the determinate of the deformation gradient.
- Up to 6 coefficients may be entered for the μi, αi, and βi terms. Values for the i = 1 coefficients are required. All other default to values.
- Values for μi, αi, and βi for i = 2, NA are required. Blank lines are not required for i > NA.
- The
βi coefficients are related to the Poisson's ration values,
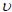i, by
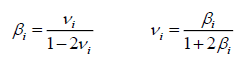
- At small strains, the initial shear modulus,
μ0 is given by
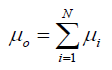
- At small strains, the initial bulk modulus,
K0 is given by
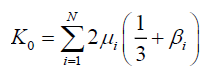
- To obtain the damping coefficient GE, multiply the critical damping ratio C/C0 by 2.0.
- TREF is used only as the reference temperature for the calculation of thermal loads.