Description
Defines material properties for use in fully nonlinear (that is, large strain and large rotation) hyperelastic analysis of rubber-like materials (elastomers) for isoparametric solid elements.
Format
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| MATHP1 | MID | MU1 | ALPHA1 | D1 | RHO | AV | TREF | GE | |
| NA | ND | ||||||||
| MU2 | ALPHA2 | D2 | MU3 | ALPHA3 | D3 | ||||
| D4 |
Example
| MATHP1 | 100 | 0.3245 | 2.0 | 1.45+4 | |||||
| 2 | 1 | ||||||||
| -0.2345 | -2.0 |
| Field | Definition | Type | Default |
|---|---|---|---|
| MID | Material identification number | Integer > 0 | Required |
| MUi | Shear moduli related to distortional deformation. | Real | 0.0 |
| ALPHAi | Exponents related to distortional deformation. | Real | 0.0 |
| Di | Material constants related to volumetric deformation. | Real ≥ 0 | See Remark 2 |
| RHO | Mass density in original configuration. | Real | 0.0 |
| AV | Volumetric coefficient of thermal expansion. | Real | 0.0 |
| TREF | Reference temperature for the calculation of thermal loads. | Real | 0.0 |
| GE | Structural element damping coefficient. See Remarks 6 and 8. | Real | 0.0 |
| NA | Order of the distortional strain energy polynomial function. | 0 < Integer ≤ 3 | 1 |
| ND | Order of the volumetric strain energy polynomial function. | 0 < Integer ≤ 4 |
Remarks
- The generalized Ogden strain energy may be expressed as follows:
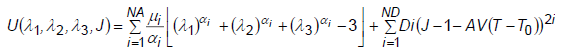
where λ1, λ2, and λ3 are principal stretches; J = detF is the determinate of the deformation gradient; and 2D1 = K at small strains, in which K is the bulk modulus. T is the current temperature and T0 is the initial temperature.
- The default for D1 is
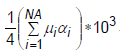. The default for D2 through D4 is zero.
- Hyperelastic materials show a fully incompressible or nearly incompressible behavior. Full incompressibility is not presently available, while nearly incompressible behavior can be simulated using a large value of D1.
- The mass density, RHO, will be used to automatically compute mass for all structural elements.
- Weight density may be used in field 9 if the value 1/g is entered on the PARAM, WTMASS entry, where g is the acceleration of gravity.
- To obtain the damping coefficient GE, multiply the critical damping ratio C/C0 by 2.0.
- TREF is used only as the reference temperature for the calculation of thermal loads in linear solutions. If TEMPERATURE(INITIAL) is specified, TREF will be ignored.
- If PARAM W4 is not specified, GE is ignored in transient response analysis. See the Parameters section for more information on W4.