Section 15: Flat Walled Tank Exercise

Introduction

In this exercise, we will conduct a nonlinear static analysis using a hydrostatic load to explore the phenomenon of stress stiffening. The subject model is a flat walled tank that is 48 inches x 48 inches x 96 inches tall. The walls of the tank are flat and are subject to pressure loading which can lead to large deformation effects.

We will run this analysis as both a linear static and a nonlinear analysis and compare the results.

1. Open the Model and Start the Autodesk Inventor Nastran Environment

Start Autodesk Inventor, and open Flat Walled Tank.ipt from the Section 15 - Flat Walled Tank sub-folder of your training exercises folder.

You should see this:

Note that this model is a quarter of the actual tank. This reduces the model to a 1/4 symmetry. Also note the feature called Split1. This is how we will control the liquid fill height of the tank. We will assume a fill height of 84 inches. Note that the "wetted" faces that experience the pressure load are colored purple.

From the Environments ribbon tab, click Autodesk Inventor Nastran. In the Model tree, expand Idealizations. If any Idealizations are already defined, like Solids 1 and 2 below, right-click Idealizations > Delete All, to ensure that no unwanted materials can participate in the analysis.

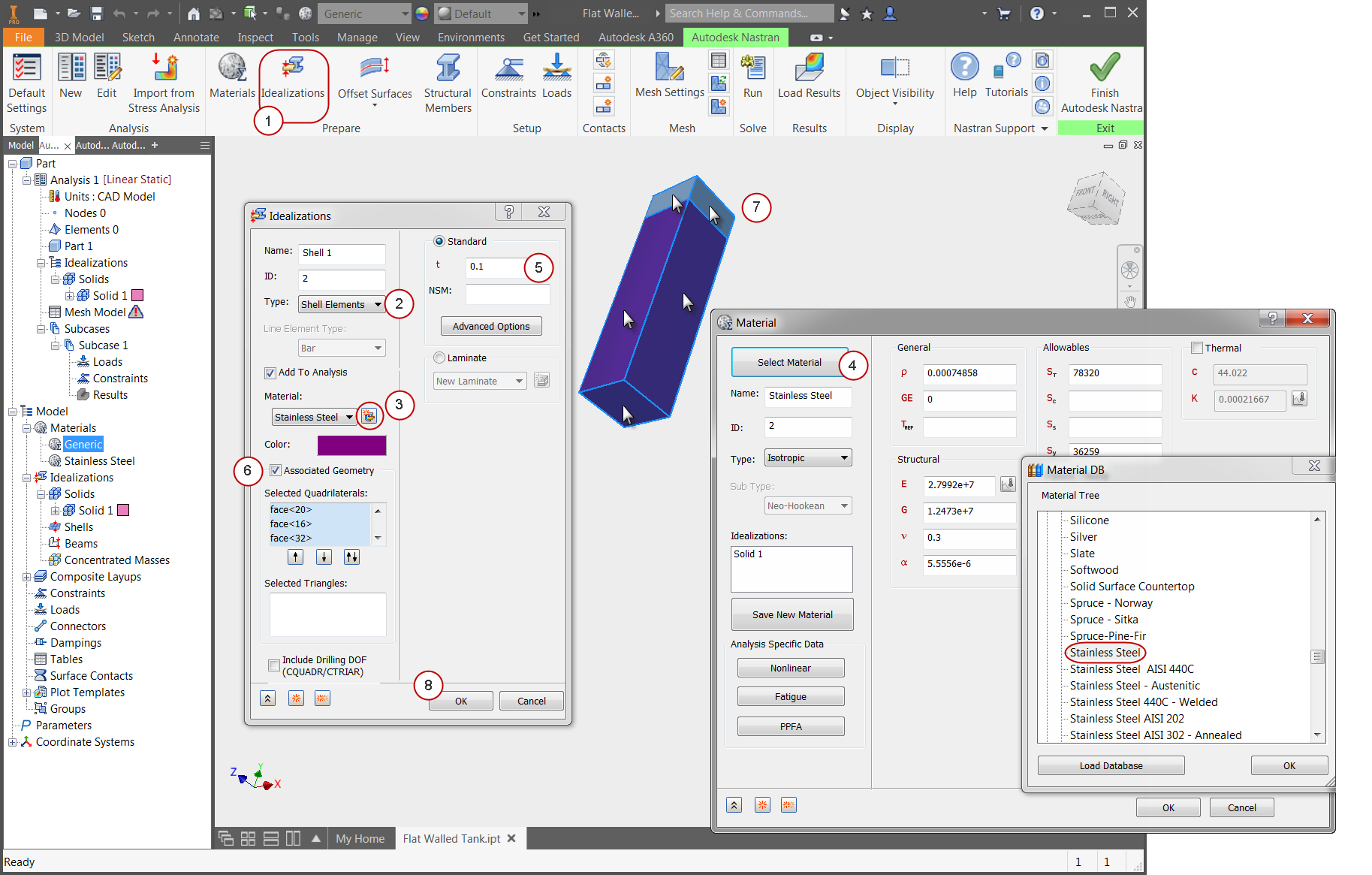
2. Define the Physical Property

  1. Click Idealizations from the ribbon.
  2. On the Idealizations dialog, set the Type to Shell Elements.
  3. Click the New Material icon.
  4. On the Material dialog, click Select Material. Expand the Autodesk Material Library, and select Stainless Steel. Click OK. Click OK on the Material dialog.
  5. On the Idealizations dialog, set the thickness, t, to 0.1.
  6. Check the Associated Geometry box.
  7. Select the five surfaces on the tank as shown.
  8. Click OK.

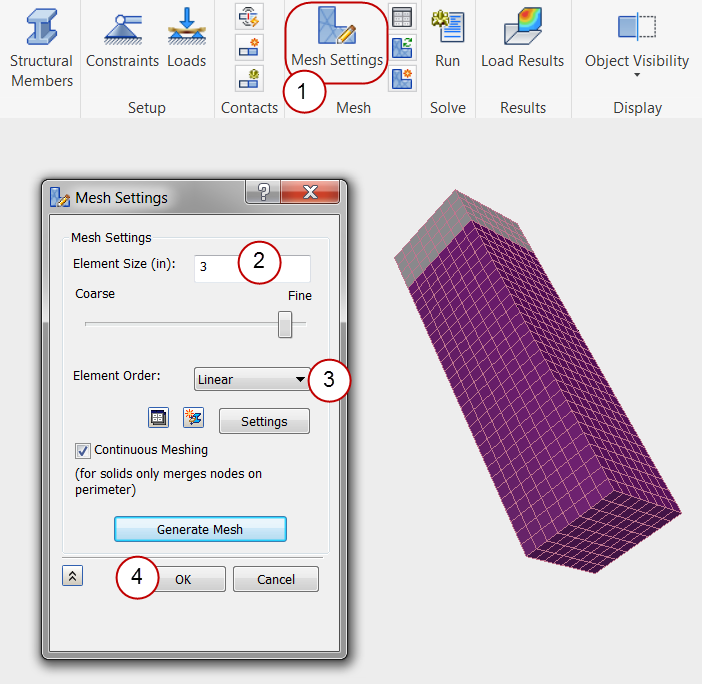
3. Mesh the Tank

  1. Click Mesh Settings from the Mesh panel of the ribbon.
  2. Enter 3 as the Element Size.
  3. Change the Element Order to Linear.
  4. Click OK to generate the mesh.

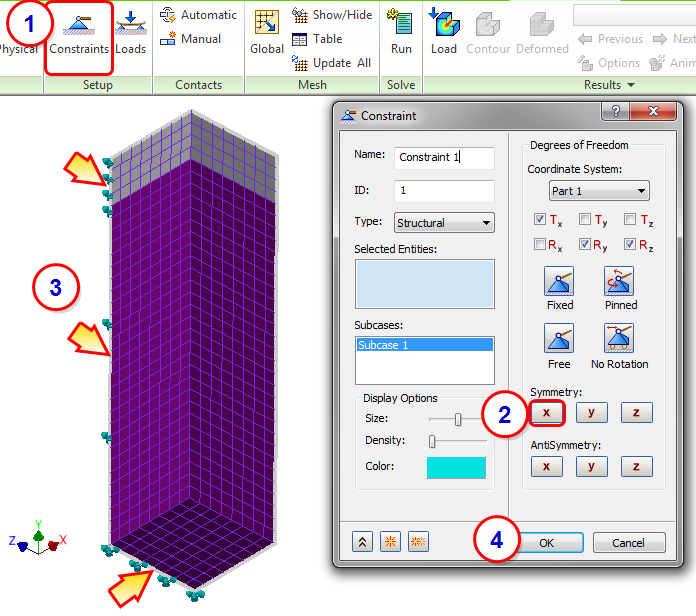
Note: If any of the five faces is not meshed, edit the property, reassign to the same five surfaces, and rebuild the mesh.

4. Constrain the Tank Edges in the YZ Plane

In this step, we will assign X symmetry to the symmetry edges in the YZ plane.

  1. Click Constraints from the ribbon.
  2. Click X Symmetry.
  3. Select the three edges shown in the image. Note the orientation of the model and the coordinate system.
  4. Click OK.

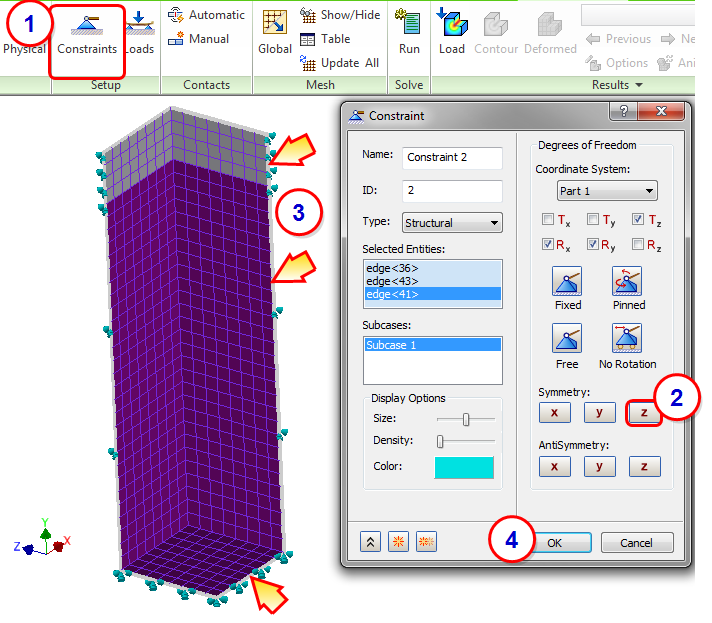
5. Constrain the Tank Edges

In this step, we will assign Z symmetry to the symmetry edges in the XY plane.

  1. Click Constraints from the ribbon.
  2. Click Z Symmetry.
  3. Select the three edges shown in the image. Note the orientation of the model and the coordinate system.
  4. Click OK.

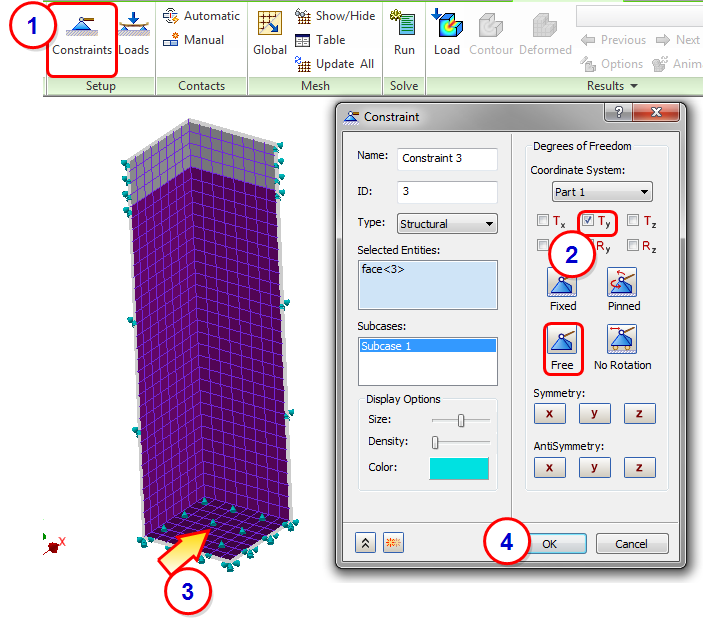
6. Constrain the Bottom of the Tank

Next we add a vertical constraint to the bottom surface to ensure the bottom surface stays on the ground. This and the two symmetry conditions allow the tank to expand naturally.

  1. Click Constraints from the ribbon.
  2. Click Free, and then Ty.
  3. Select the bottom surface of the tank.
  4. Click OK.

7. Assign the Pressure Load

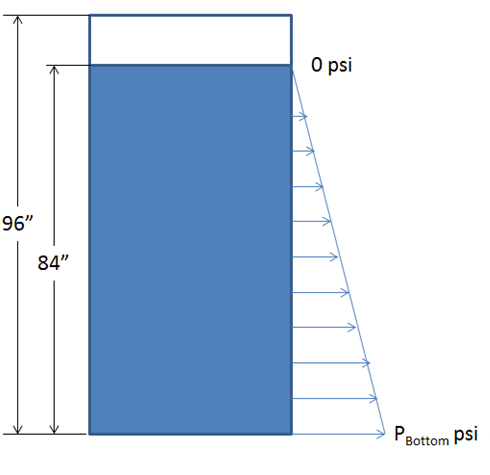
The hydrostatic load will simulate the tank filled with 84 inches of water. The geometry is split so that a point on the free surface of the water can be selected.

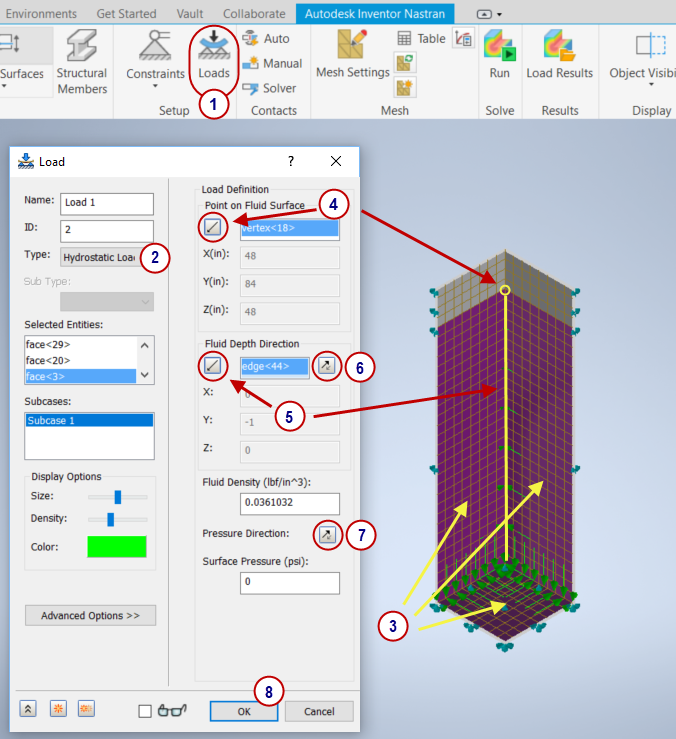
  1. Click Loads from the Setup panel of the ribbon.
  2. Select Hydrostatic Load as the Type.
  3. Select the three wetted surfaces of the tank.
  4. Click the Point on Fluid Surface selector, then click one of the 3 corner vertices at the top of the fluid.
  5. Click the Fluid Depth Direction selector, then click a vertical edge on the tank. Note the Y value of 1, indicating that fluid depth increases in the positive Y direction, moving upward in the tank.
  6. Click the Fluid Depth Direction Reverse Direction button to change the direction of the fluid pressure to negative Y, moving downward in the tank.
  7. Click Pressure Direction to reverse the direction of the pressure so that the water is inside the tank instead of outside the tank.
  8. Click OK.

8. Run a Linear Static and Review the Results

  1. Click Run from the ribbon.
  2. From the Results branch of the Analysis tree, right-click on Displacement, and click Display.

  3. Right-click on von Mises, and click Display.

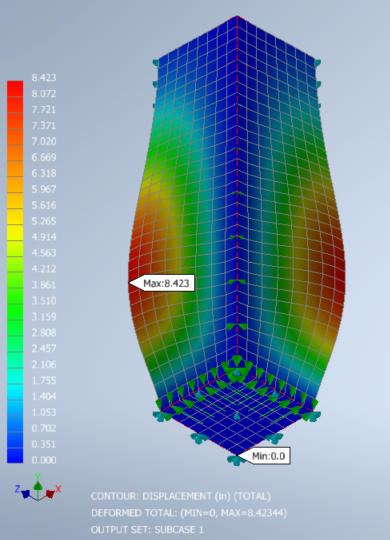
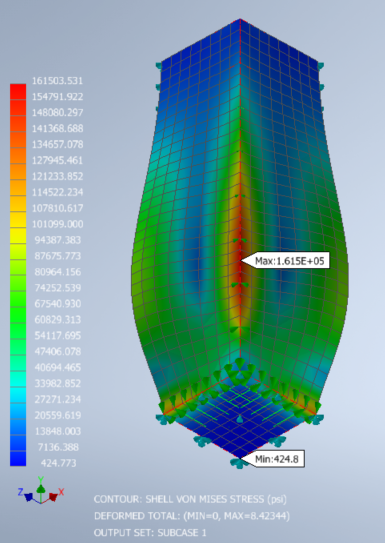
Both the displacement and the von Mises stress results plots show that there are problems with the tank.

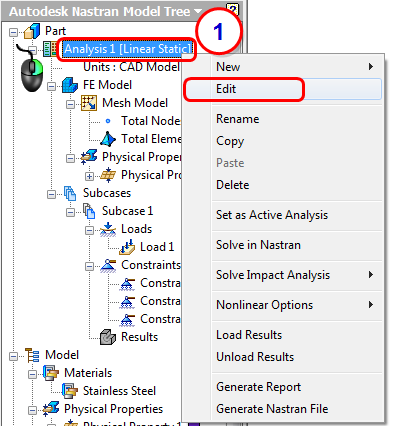
9. Change the Analysis Type to Nonlinear Static and Rerun

  1. Right-click on Analysis 1 in the Analysis tree, and click Edit.

  2. Change the Type to Nonlinear Static.
  3. Click OK.
  4. Click Run from the ribbon.

10. Review Nonlinear Results

  1. Right-click on Results in the Analysis tree, and click Edit.
  2. Select Displacement.

  3. Click the Deform Options tab. Select Actual, and specify a Value of 1.0.
  4. Click Display.

  5. Click the Contour Options tab. Change Result Data to Stress, and change Type to SHELL MAX VON MISES STRESS BOTTOM/TOP. (If the results do not update, click Display.)

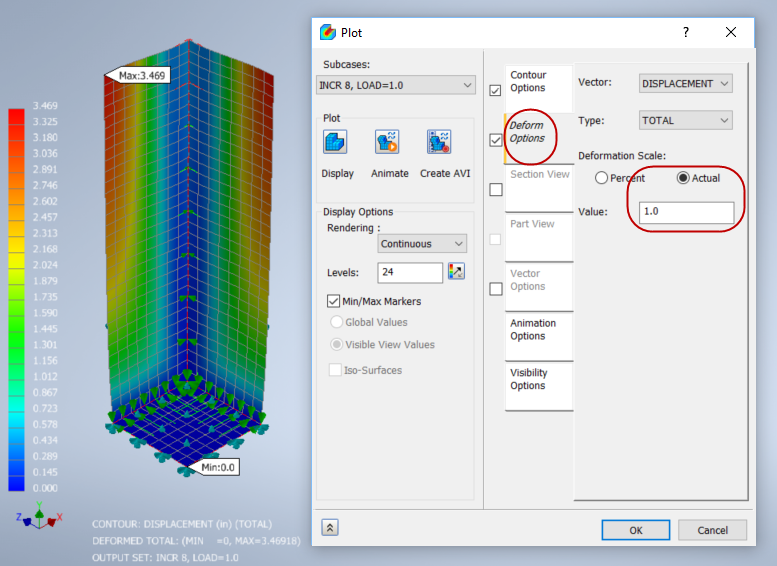
The results look significantly different from the linear static results!

Summary

In this exercise, we compared linear and nonlinear results for a large displacement model to demonstrate how we can obtain better accuracy by switching to the Nonlinear Static analysis type. Additionally, we used symmetry constraints on a shell model, and defined shell properties on a solid face. To simulate the variation of hydrostatic pressure with depth, we applied a hydrostatic load to the vertical wetted surfaces of the tank.

Previous Topic: Nonlinear Static Analysis

Next Topic: Nonlinear Transient Analysis

Parent topic: Section 14: Nonlinear Static Analysis