Returning the log files, make note of the volume fraction assigned and calculated during the homogenization and meshing process:
STL file start pre-processing Homogenizing STL 2... Reading Lattice.stl Reading in native format... Binary STL file Bounding box: 2.172730E+00 <= x <= 2.777782E+01 2.172791E+00 <= y <= 2.777775E+01 5.929890E-01 <= z <= 1.943214E+01 Number of vertices = 222,600 Number of triangles = 74,200 Finished reading Lattice.stl Equivalencing vertices Number of unique vertices = 35,972 Finished vertex equivalencing Original STL volume = 149.531685569228 Seeding STL vertices with max length 8.00000000000000... Number of seeded points = 35,972 Pseudo-randomizing vertex ordering...
Getting Delaunay triangulation for 35972 points... Number of tetrahedrons = 248850 Wall time for tetrahedralization = 0.91153 Alpha radius = 10.0000000000000 Filtering 2187 tetrahedrons... Number of hull triangles = 2662 Finished writing binary STL file Lattice_concavity.stl Homogenized STL volume = 8639.01118122283 Volume fraction = 1.7308889E-02 Homogenizing STL 3... Reading Support1_Solid.stl Reading in native format... Binary STL file Bounding box: -9.002001E+00 <= x <= 1.000000E+00 1.000000E+01 <= y <= 2.000000E+01 0.000000E+00 <= z <= 1.943000E+01 Number of vertices = 93,636 Number of triangles = 31,212 Finished reading Support1_Solid.stl Equivalencing vertices Number of unique vertices = 14,276 Finished vertex equivalencing Seeding STL vertices with max length 12.0000000000000... Number of seeded points = 14,332 Pseudo-randomizing vertex ordering...
Getting Delaunay triangulation for 14332 points... Number of tetrahedrons = 84955 Wall time for tetrahedralization = 0.26255 Alpha radius = 15.0000000000000 Filtering 604 tetrahedrons... Number of hull triangles = 4648 Finished writing binary STL file Support1_Solid_concavity.stl Volume fraction = 0.2200000 Homogenizing STL 4... Reading Support2_0Thickness_Loose.stl Reading in native format... Binary STL file Bounding box: 1.743000E+01 <= x <= 3.065200E+01 2.484200E+01 <= y <= 3.813200E+01 0.000000E+00 <= z <= 1.940400E+01 Number of vertices = 17,937 Number of triangles = 5979 Finished reading Support2_0Thickness_Loose.stl Equivalencing vertices Number of unique vertices = 5051 Finished vertex equivalencing Calculating surface normals Original STL surface area = 462.472214730474 Original STL volume = 101.743887240704 Seeding STL vertices with max length 4.00000000000000... Number of seeded points = 5120 Pseudo-randomizing vertex ordering...
Getting Delaunay triangulation for 5120 points... Number of tetrahedrons = 28056 Wall time for tetrahedralization = 0.0910063 Alpha radius = 5.00000000000000 Filtering 451 tetrahedrons... Number of hull triangles = 2964 Finished writing binary STL file Support2_0Thickness_Loose_concavity.stl Homogenized STL volume = 924.134388621194 Volume fraction = 0.1100964 Homogenizing STL 5... Reading Support3_0Thickness_Fine.stl Reading in native format... Binary STL file Bounding box: 1.731400E+01 <= x <= 3.065600E+01 -7.656000E+00 <= y <= 5.682000E+00 0.000000E+00 <= z <= 1.937400E+01 Number of vertices = 73,137 Number of triangles = 24,379 Finished reading Support3_0Thickness_Fine.stl Equivalencing vertices Number of unique vertices = 19,241 Finished vertex equivalencing Calculating surface normals Original STL surface area = 1113.08966895905 Original STL volume = 166.963450343858 Seeding STL vertices with max length 4.00000000000000... Number of seeded points = 19,409 Pseudo-randomizing vertex ordering...
Getting Delaunay triangulation for 19409 points... Number of tetrahedrons = 114150 Wall time for tetrahedralization = 0.390239 Alpha radius = 5.00000000000000 Filtering 2006 tetrahedrons... Number of hull triangles = 7888 Finished writing binary STL file Support3_0Thickness_Fine_concavity.stl Homogenized STL volume = 933.467339324015 Volume fraction = 0.1788637
For each of the four homogenized geometries, the solve calculates the original STL volume and the homogenized volume. For all but the solid support structure, the volume fraction is then calculated. For the solid support structure the volume fraction has been directly assigned and is reported as 0.22. The volume fractions are:
- Lattice – 0.0173
- Solid support – 0.22
- Loose zero thickness support – 0.11
- Fine zero thickness support – 0.178
Figure 3 displays the displacement results of the thermo-mechanical simulation at the end of the build process, after part cool-down. The part has been warped by displacement with no additional magnification. The support structure to the fore of the picture is the Solid support, assigned a volume fraction of 0.22, to the left is the Loose zero-thickness support, with a calculated volume fraction of 0.11, and to the right the Fine zero thickness support, with the largest volume fraction, calculated to be 0.178. The Solid and Fine supports exhibit an equivalent trend and value of distortion, while the Loose lattice-type support shows roughly 25% more distortion than the other supports.

Figure 3: STL homogenization example displacement results
Figure 4 gives the structure type results at the end of the simulation, which is most useful in this case for investigating support structure failures. The figure has been filtered to show only the support structure and failed support structure types. This shows that these disparate support types all exhibit similar levels of failure.
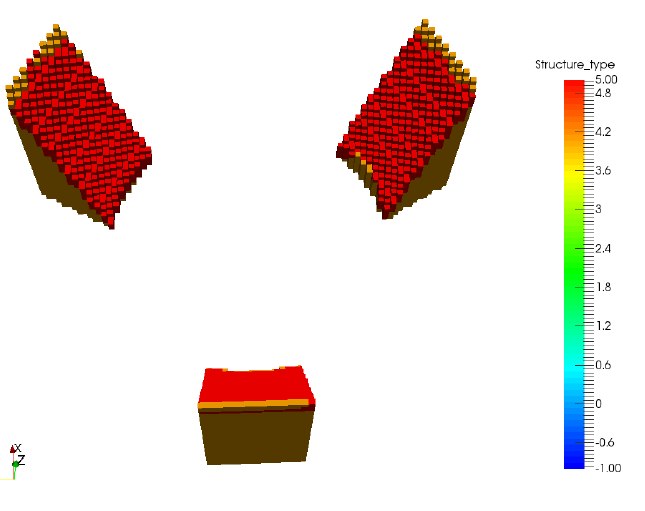
Figure 4: STL homogenization example support failure results