The Large Displacements Analysis of Shell Structures allows for arbitrarily large displacements and rotations in a structure discretized by means of shell elements. The corotational approach has been employed.
A single element may be subjected to arbitrarily large displacements and rotations as a rigid body, but the true deformation (which generates strains, and in consequence stresses) remains small within one element. The element interior geometrical relationships remain linear. Geometrical non-linearity is treated on the level of the structure.
It enables the use of existing finite elements with all their feasibilities.
The idea is to deduct its part associated with rigid motion (not generating strains and stresses) from the total element deformation. Resulting stresses and element forces are evaluated for the true part of the deformation.
Element processing is performed with respect to the element frame {E} rigidly attached with the displacing element. Afterward, calculated forces and the stiffness matrix are transformed to the global system.
Deduction of rigid body motion is equivalent to the projection. The sequence of operations performed on the displacement increments, forces, and the element stiffness matrix is illustrated as follows.
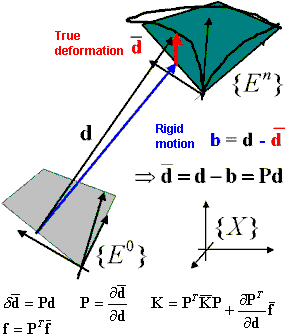
Rotations are treated as arbitrarily large. A rotation is represented by a tensor. Rodriguez formula (exponential mapping) is applied for transformations from the pseudo-vector w to the rotation tensor Q. During an update of rotational degrees of freedom, a product of rotation tensors is used instead of adding up rotation vectors.