Las curvas de recorte tienen dos restricciones principales:
- Es necesario que la curva esté situada en la superficie. Para contener una curva en una superficie se recomienda:
- Si la superficie es una superficie plana, modele la curva en el plano de la curva.
- Proyecte una curva sobre la superficie.
- Interseque dos superficies para obtener una curva.
- Es necesario que la curva divida la superficie en dos zonas distintas. De lo contrario, se obtendrá el error Imposible recortar: la curva de recorte no finaliza en un límite. Considere que la superficie es una hoja de papel y la curva de recorte la trayectoria de unas tijeras. Después de cortar, quedan dos trozos de papel. La curva de recorte tiene que poder hacer una de las siguientes opciones:
- Formar un bucle en el interior de la superficie
- Cortar los límites de dos superficies
- Cortar el mismo límite dos veces
Ejemplos de recorte:
Válido: 
Válido: 
Válido: 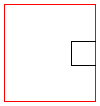
No válido: 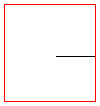
Restricciones adicionales del recorte:
- No incluya partes del límite al construir curvas de recorte. Puede que estas curvas crucen o terminen en los límites.
- Evite cortar a través del límite mal generado en superficies como el polo de una esfera o una superficie de revolución.
- Evite cortar a lo largo del cosido de una superficie (puede hacerlo transversalmente). Un cosido existe, por ejemplo, en el límite izquierdo/derecho de un cilindro. Los cosidos pueden detectarse con el cuadro de diálogo Límite de superficies, cancelándolo una vez que se sepa dónde está el cosido. Evite cortar un cosido girando el objeto porque los objetos con cosidos suelen ser simétricos.