Fórmulas de cálculo de tolerancia

Consejo: Para sus cálculos de análisis de tolerancia 1D, considere la posibilidad de usar el complemento Análisis de tolerancia de Autodesk® Inventor®. Análisis de tolerancia de Inventor ofrece un completo conjunto de herramientas que le ayuda a comprender con más claridad el impacto del ajuste mecánico y el rendimiento en función de la variación dimensional acumulada.

Para obtener más información, consulte Para definir acumulaciones de tolerancia.

Obtenga las ecuaciones básicas para cadenas lineales cerradas de cotas a partir de la siguiente imagen.

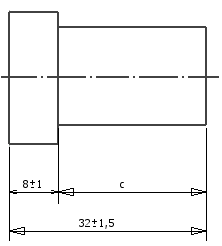
a = 32 ± 1,5 mm, b = 8 ± 1 mm

Elementos ascendentes/descendentes

Si el elemento ascendente aumenta, el elemento de cierre también lo hace. Si el elemento descendente aumenta, el elemento de cierre disminuye si el resto de elementos de la cadena permanezcan constantes.

Elemento de cierre:	1. c = a - b
Límite de cota superior del elemento de cierre:	2. c máx = a máx - b mín
Límite de cota inferior del elemento de cierre:	3. c mín = a mín - b máx
Tolerancia del elemento de cierre (restando la ecuación 3 de la ecuación 2)	4. c máx - c mín = a máx - a mín - (b mín - b máx )
Como	5. T c = T a + T b

Nota: La tolerancia del elemento de cierre equivale a la suma de tolerancias de todos los elementos de la cadena de cotas cerradas.

En general, las tolerancias de la cadena lineal cumplen la siguiente ecuación.

De forma análoga, las ecuaciones 2 y 3 se pueden escribir de modo general.

El límite de cota superior del elemento de cierre equivale a la diferencia de la suma de los límites de cota superiores de los elementos ascendentes y la suma de los límites de cota inferiores de los elementos descendentes.

El límite de cota inferior del elemento de cierre equivale a la diferencia de la suma de los límites de cota inferiores de los elementos ascendentes y la suma de los límites de cota superiores de los elementos descendentes.

La cota nominal del elemento de cierre se puede expresar mediante la ecuación 1, tal como se muestra en la siguiente ecuación.

Límite de desviación superior del elemento de cierre.

Límite de desviación inferior del elemento de cierre.