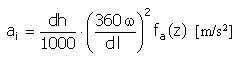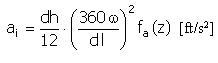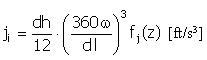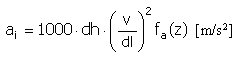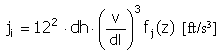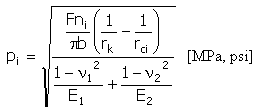Datos de entrada:
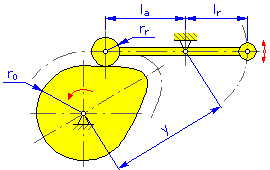
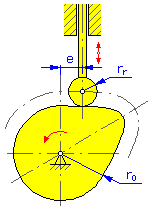
- Radio básico r 0 (levas cilíndricas y de disco)
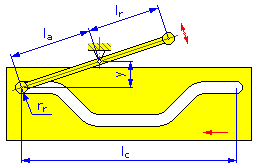
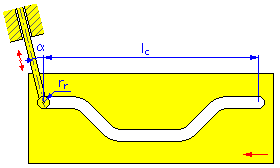
- Longitud del movimiento l c (levas lineales)
- Anchura de la leva b c
- Radio del rodillo r r
- Anchura del rodillo b r (para el cilindro de forma del seguidor)
- Excentricidad e (levas de disco para trasladar el seguidor)
- Ángulo de excentricidad α (levas de disco lineales y cilíndricas para trasladar el seguidor)
- Distancia de giro y (levas de disco y lineales para el brazo oscilante)
- Longitud del brazo l a (levas de disco y lineales para el brazo oscilante)
- Brazo de reacción l r (levas de disco y lineales para el brazo oscilante)
- Velocidad ω (levas de disco y cilíndricas)
- Velocidad v (levas lineales)
- Fuerza sobre rodillo F
- Peso acelerado m
- Capacidad del muelle c
- Presión admitida p A1
- Módulo de elasticidad del material de la leva E 1
- Coeficiente de Poisson del material de la leva μ 1
- Presión admitida p A2
- Módulo de elasticidad del material del seguidor E 2
- Coeficiente de Poisson del material del seguidor μ 2
|
Leva de disco |
|
|
|
|
|
Leva lineal |
|
|
|
|
|
Leva cilíndrica |
|
 |
|
|
Diámetro exterior = 2r 0 + b c |
|
|
Diámetro interior = 2r 0 - b c |
|
Segmentos de la leva
- Función de movimiento f y (z) [ul]
- Coeficiente marcha atrás k r (solo para el movimiento parabólico y parabólico con parte lineal)
- Coeficiente de parte lineal k l (solo para el movimiento parabólico con parte lineal)
- Posición inicial de movimiento l 0 [°; mm, pulg.]
- Posición final de movimiento l [°; mm, pulg.]
- Longitud de movimiento del segmento dl = l - l 0 [°; mm, pulg.]
- Elevación al inicio h 0 [mm, pulg.]
- Elevar al final h máx [mm, pulg.]
- Elevar segmento d h = h máx - h 0 [mm, pulg.]
Dependencias de elevación
Leva de disco y cilíndrica
Ángulo de rotación de la leva ϕ i [°]
Posición relativa real en el segmento: z i = (ϕ i - l 0 ) / dl (rango 0 - 1)
|
Elevación |
y i = dh f y (z) [mm, pulg.] |
|
Velocidad |
|
|
|
|
|
Aceleración |
|
|
|
|
|
Impulso |
|
|
|
Leva lineal
Posición de movimiento de la leva l i [mm, pulg.]
Posición relativa real en el segmento: z i = (l i - l 0 ) / dl (rango 0 - 1)
|
Elevación |
y i = dh f y (z) [mm, pulg.] |
|
Velocidad |
|
|
Aceleración |
|
|
|
|
|
Impulso |
|
|
|
Funciones de movimiento
Cicloidal (sinusoidal ampliado)
Este movimiento tiene unas excelentes características de aceleración. Se usa a menudo en las levas de alta velocidad porque genera unos niveles bajos de ruido, vibración y desgaste.

|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
|
Elevación |
f y (z) = z - 0.5/π sin(2πz) |
|
Velocidad |
f v (z) = 1 - cos (2πz) |
|
Aceleración |
f a (z) = 2π sin(2πz) |
|
Impulso |
f j (z) = 4π 2 cos(2πz) |
Armónico (sinusoidal)
La ventaja inherente a esta curva es la uniformidad de la velocidad y la aceleración durante el recorrido. Sin embargo, los cambios instantáneos de la aceleración al principio y al final del movimiento suelen provocar vibración, ruido y desgaste.

|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
|
Elevación |
f y (z) = 0.5 (1 - cos πz)) |
|
Velocidad |
f v (z) = 0.5 π sin (πz) |
|
Aceleración |
f a (z) = 0.5 π 2 cos(πz) |
|
Impulso |
f j (z) = -0.5π 3 sin(πz) |
Lineal
Movimiento simple con un enorme impacto al principio y al final del movimiento. No se usa casi nunca, salvo en dispositivos muy rudimentarios. Es aconsejable usar un movimiento con un principio y un final modificados (parabólico con una parte lineal).

|
|
Elevación |
|
|
Velocidad |
|
Elevación |
f y (z) = z |
|
Velocidad |
f v (z) = 1 |
|
Aceleración |
f a (z) = 0 |
|
Nota: Para z = 0 y z = 1, el valor correcto debería ser un valor infinito, pero el cálculo no funciona con valores infinitos, por lo que utiliza un valor cero.
|
|
|
Impulso |
f j (z) = 0 |
|
Nota: Para z = 0 y z = 1, el valor correcto debería ser un valor infinito, pero el cálculo no funciona con valores infinitos, por lo que utiliza un valor cero.
|
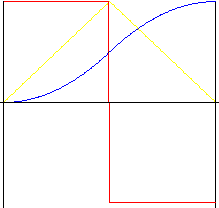
Parabólico (polinomio de 2 º grado)
Movimiento con la menor aceleración posible. Sin embargo, a causa de los cambios de aceleración repentinos que se dan al principio, en la parte central y al final del movimiento, se producen impactos. El coeficiente inverso permite que en el “tramo” central del movimiento se produzca un cambio en la proporción entre aceleración y deceleración.
simétrico (coeficiente inverso k r = 0,5)
|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
para z = 0 a 0,5: |
|||
|
Elevación |
fy(z) = 2z 2 |
||
|
Velocidad |
fv(z) = 4z |
||
|
Aceleración |
fa (z) = 4 |
||
|
Impulso |
fa(z) = 0 |
||
|
para z = 0,5 - 1: |
|||
|
Elevación |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Velocidad |
fv(z) = 4 (1 - z) |
||
|
Aceleración |
fa (z) = -4 |
||
|
Impulso |
fj(z) = 0 |
||
|
Nota: Para z = 0 y z = 1, el valor correcto debería ser un valor infinito, pero el cálculo no funciona con valores infinitos, por lo que utiliza un valor cero.
|
|||
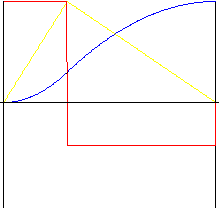
no simétrico
k r - coeficiente inverso (en el rango 0,01 a 0,99)
|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
para z = 0 a k r : |
|||
|
Elevación |
f y (z) = z 2 / k r |
||
|
Velocidad |
f v (z) = 2z / k r |
||
|
Aceleración |
f a (z) = 2 / k r |
||
|
Impulso |
f j (z) = 0 |
||
|
para z = k r a 1: |
|||
|
Elevación |
f y (z) = 1 – (1 – z) 2 / (1 – k r ) |
||
|
Velocidad |
f v (z) = 2 (1 – z) / (1 – k r ) |
||
|
Aceleración |
f a (z) = -2 / (1 - k r ) |
||
|
Impulso |
f j (z) = 0 |
||
|
Nota: Para z = 0 y z = 1, el valor correcto debería ser un valor infinito, pero el cálculo no funciona con valores infinitos, por lo que utiliza un valor cero.
|
|||
Parabólico con parte lineal
Proporciona una aceleración y una deceleración más aceptables que las del movimiento lineal. El coeficiente inverso permite que en el “tramo” central del movimiento se produzca un cambio en la proporción entre aceleración y deceleración. El coeficiente de la parte lineal permite establecer el tamaño relativo de la parte lineal del movimiento.

|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
k r - coeficiente inverso (en el rango 0,01 a 0,99)
k l - coeficiente de la parte lineal (en el rango 0 a 0,99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
para z = 0 a k r / k z : |
|||
|
Elevación |
f y (z) = k h z 2 k z 2 / k r |
||
|
Velocidad |
f v (z) = 2 k h z k z 2 / k r |
||
|
Aceleración |
f a (z) = 2 k h k z 2 / k r |
||
|
Impulso |
f j (z) = 0 |
||
|
para z = k r / k z a r / k z + k l : |
|||
|
Elevación |
f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l ) |
||
|
Velocidad |
f v (z) = 2 / (1 + k l ) |
||
|
Aceleración |
f a (z) = 0 |
||
|
Impulso |
f j (z) = 0 |
||
|
para z = k r / k z + k l a 1: |
|||
|
Elevación |
f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Velocidad |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Aceleración |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Impulso |
f j (z) = 0 |
||
Polinomio de 3 er grado (parábola cúbica)
Movimiento con impactos más pequeños que el movimiento parabólico.

|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
|
Elevación |
f y (z) = (3 -2z) z 2 |
|
Velocidad |
f v (z) = (6 - 6z) z |
|
Aceleración |
f a (z) = 6 - 12z |
|
Impulso |
f j (z) = -12 |
Polinomio de 4 º grado
Movimiento con impactos más pequeños que el movimiento del polinomio de tercer grado.

|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
|
para z = 0 - 0,5 |
||
|
Elevación |
f y (z) = (1 - z) 8z 3 |
|
|
Velocidad |
f v (z) = (24 - 32z) z 2 |
|
|
Aceleración |
f a (z) = (48 - 96z) z |
|
|
Impulso |
f j (z) = 48 - 192z |
|
|
para z = 0,5 - 1 |
||
|
Elevación |
f y (z) = 1 - 8z (1 - z) 3 |
|
|
Velocidad |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Aceleración |
f a (z) = (48 - 96z) (1 - z) |
|
|
Impulso |
f j (z) = 194z - 144 |
|
Polinomio de 5 º grado
Movimiento con impactos más pequeños que el movimiento del polinomio de tercer grado.

|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
|
Elevación |
f y (z) = (6z 2 - 15z + 10) z 3 |
|
Velocidad |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Aceleración |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Impulso |
f j (z) = (6z 2 - 6z + 1) 60 |
Polinomio de 7 º grado
Uniformidad en todas las fórmulas, incluido el impulso.

|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
|
Elevación |
f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Velocidad |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Aceleración |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Impulso |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
Polinomio no simétrico de 5 º grado
Similar al polinomio de 5º grado, pero con una inversión forzada de la elevación.
|
|
Elevación |
|
|
Velocidad |
|
|
Aceleración |
|
|
Impulso |
|
Pieza 1 |
||
|
Elevación |
f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Velocidad |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Aceleración |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Impulso |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Pieza 2 |
||
|
Elevación |
f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Velocidad |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Aceleración |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Impulso |
f j (z) = (4z 2 - 3z) 40 |
|
Doble armónico
Uniformidad en todas las fórmulas, incluido el impulso con inversión forzada de la elevación.

|
Pieza 1 |
||
|
Elevación |
f y (z) = cos(0,5π (1 - z)) 4 |
|
|
Velocidad |
f v (z) = π (0,5 sin(πz) - 0,25 sin(2πz)) |
|
|
Aceleración |
f a (z) = 0,5 π 2 (cos(πz) - cos(2πz)) |
|
|
Impulso |
f j (z) = π 3 (-0,5 sin(πz) + sin(2πz)) |
|
|
Pieza 2 |
||
|
Elevación |
f y (z) = 1 - cos(0,5π z) 4 |
|
|
Velocidad |
f v (z) = π (0,5 sin(πz) + 0,25 sin(2πz)) |
|
|
Aceleración |
f a (z) = 0,5 π 2 (cos(πz) + cos(2πz)) |
|
|
Impulso |
f j (z) = -π 3 (0,5 sin(πz) + sin(2πz)) |
|
Comparación de los valores relativos máximos
|
Movimiento |
Velocidad |
Aceleración |
Impulso |
|
Cicloidal (sinusoidal ampliado) |
2 |
6,28 |
39,5 |
|
Armónico (sinusoidal) |
1,57 |
4,93 |
15,5 |
|
Lineales |
1 |
∞ |
∞ |
|
Parabólico (polinomio de 2 º grado) |
2 |
4 |
∞ |
|
Polinomio de tercer grado |
1,5 |
6 |
12 |
|
Polinomio de 4 º grado |
2 |
6 |
48 |
|
Polinomio de 5 º grado |
1,88 |
5,77 |
60 |
|
Polinomio de 7 º grado |
2,19 |
7,51 |
52,5 |
|
Polinomio no simétrico de 5 º grado |
1,73 |
6,67 |
40 |
|
Doble armónico |
2,04 |
9,87 |
42,4 |
Otras dependencias
Fuerza sobre el rodillo
|
F i = F + m a i + c y i [N, lb] |
Fuerza normal
|
Fn i = F i / cos (γ i ) [N, lb] |
Momento
|
T i = F i r i tan (γ i ) [Nmm, lb pulg.] |
Presión específica (hertzios)
|
|
|
|
b = min (b v, b k ) |