En el rodamiento se origina energía térmica debido a pérdidas por fricción. La energía está en equilibrio con el calor conducido desde el rodamiento. El calor se transfiere desde el rodamiento pasando desde el eje y la superficie del alojamiento del rodamiento al entorno. El tránsito del calor se realiza mediante conducción y emisiones, y principalmente pasa al lubricante fluido.
La mayor parte del calor originado (se estima que más del 75%) es conducido desde el rodamiento a través del lubricante. Por este motivo, la temperatura del lubricante aumenta desde que entra hasta que sale del rodamiento, a medida que lo atraviesa. La finalidad del cálculo del equilibrio térmico del rodamiento es encontrar una temperatura media del lubricante en la salida del rodamiento a la que el lubricante seleccionado pueda mantener en equilibrio la energía térmica que se origina debido a la fricción con el calor que se transporta desde el rodamiento.
La cantidad de calor que el lubricante transporta desde el rodamiento depende de la densidad y la viscosidad del lubricante. Debido a que tanto la densidad como la viscosidad del lubricante se ven modificadas simplemente por el cambio de temperatura, es preciso emplear un método de aproximación constante para calcular la temperatura de salida del lubricante. La temperatura de salida del lubricante esperada, propuesta por el usuario, se emplea como base para el proceso de iteración del cálculo. El cálculo repetido finaliza cuando la diferencia entre la temperatura esperada y la temperatura calculada es menor de 2 grados centígrados. Las diferencias mayores no se pueden ignorar, ya que tienen como resultado un cambio significativo en la viscosidad del aceite y la capacidad de carga de la capa de aceite.
Todas las ecuaciones de cálculo que se emplean en el equilibrio térmico se presentan en el siguiente texto:
Descarga de aceite lateral debida a la presión hidrodinámica
Si el rodamiento no está apretado en las aristas, el aceite se filtra a través del hueco de lubricación de las aristas debido a la presión hidrodinámica. El volumen de filtrado del aceite es:
V z = 0.125 R * 1 ε d 3 φω 10 -3 [cm 3 s -1 ]
donde el número característico de la descarga R * 1 se determina a partir del diagrama correspondiente para la anchura relativa del rodamiento, la excentricidad relativa del cojinete transversal y el ángulo de entrada del lubricante.

Descarga de aceite debida a la presión de entrada
Si el aceite se suministra en el rodamiento con presión de entrada, la descarga de aceite aumenta con el valor correspondiente. El volumen de aceite que se escapa debido a la presión de entrada se determina en los rodamientos lubricados mediante una ranura radial (es decir, circunferencial), con la siguiente ecuación:

en los rodamientos lubricados mediante un agujero de lubricación o una ranura de lubricación axial:
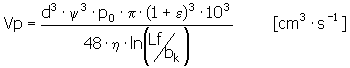
Cantidad de aceite en circulación
Parte del aceite, que se encontraba en la capa de vacío, vuelve a la capa de presión y se mantiene en circulación. La cantidad de aceite
V z = 0.125 R * 2 ε d 3 φω 10 -3 [cm 3 s -1 ]
depende del número de recirculación característico R * 2 , que se puede encontrar en el diagrama a partir de la anchura relativa del rodamiento y la excentricidad relativa del cojinete transversal:

Cantidad total de lubricante descargado en el rodamiento
La cantidad total de lubricante se determina según las siguientes condiciones:
- Suministro de lubricante sin presión y con recirculación. Solo se añade la pérdida debida a la descarga lateral.
V = V z [cm 3 s -1 ]
- Suministro de lubricante sin presión y sin recirculación. El aceite que pasa a través de la capa de lubricación se escurre o elimina debido a la refrigeración.
V = V z + V u [cm 3 s -1 ]
- Entrada de aceite con presión y con recirculación.
V = V z + V p [cm 3 s -1 ]
- Entrada de aceite con presión y con escurrido o barboteo de aceite caliente.
V = V z + V p + u [cm 3 s -1 ]
Llenado de la parte de vacío de la ranura
La capa fina de aceite, que es continua en la parte de presión de la capa de lubricación, comienza a desintegrarse al tiempo que la ranura del rodamiento comienza a llenarse con vapor de aceite y con el aire que se expulsa desde el aceite y se absorbe a través de las aristas del rodamiento. Cuanto más se vaporiza la capa fina de aceite en la parte de vacío, más se reducen las pérdidas debidas a la fricción. La liberación o retirada de la parte del casquillo sin carga contribuye a la desintegración de la fina capa de aceite. Por el contrario, el llenado completo de la ranura de lubricación tiene lugar cuando se dan las dos condiciones siguientes:
p o > 0,4 [MPa]
![]()
Las pérdidas debidas a la fricción alcanzan su máximo nivel en estas condiciones.
Coeficiente de fricción
Para el llenado parcial de la ranura de lubricación:
μ = φΜ * 1 [-]
Para el llenado total de la ranura de lubricación:
μ = φΜ * 2 [-]
Donde los números de fricción característicos M * 1 y M * 2 se determinan a partir de un diagrama para la anchura relativa del rodamiento y la excentricidad relativa del cojinete transversal:
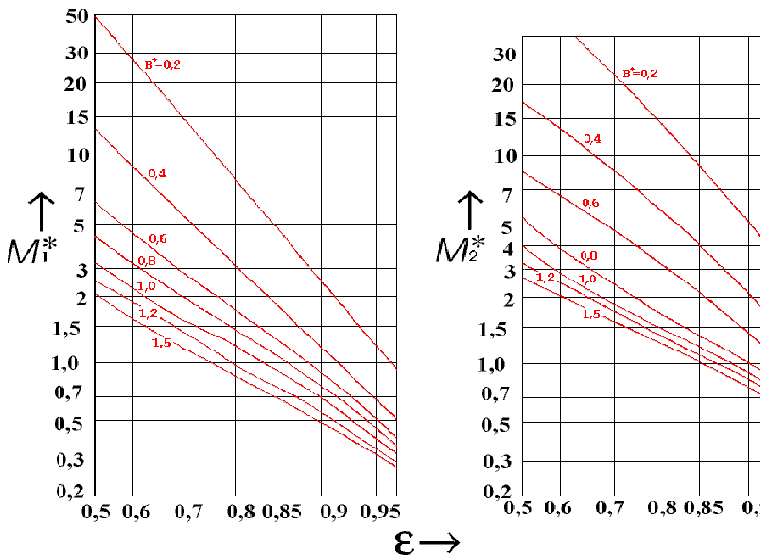
Pérdida de potencia en el rodamiento por fricción
![]()
La potencia de fricción conducida a las áreas circundantes es
P U = 3.5 π d L α W (T V - T U ) 10 -6 [W]
donde el factor de eliminación del calor es
α W = 12 + 8 ν V / 1.2 [W m -2 K -1 ] para ν V ≤ 1.2 m s -1
![]()
para ν V ≤ 1.2 m s -1
La capacidad térmica específica del lubricante correspondiente a su temperatura media en la salida del rodamiento es
c T = 4.588 T V - 5.024.10 -3 ρ 2 20 + 7.1156 ρ 20 - 619.646 [J kg -1 K -1 ]
La densidad del lubricante correspondiente a su temperatura media en la salida del rodamiento es
ρ T = ρ 20 - 0.65 (T - 20) [kg m -3 ]
El calentamiento del lubricante entre la entrada y la salida es
![]()
donde el factor de refrigeración interna que expresa el calor relativo conducido desde el rodamiento es:

La temperatura media calculada del lubricante a la salida del rodamiento es
T v = T o + ΔT [°C]
Significado de las variables utilizadas:
|
b k |
diámetro del agujero de lubricación o longitud de acanalado axial de lubricación [mm] |
|
d |
diámetro de cojinete transversal [mm] |
|
Δd |
juego diametral [mm] |
|
F |
fuerza de carga [N] |
|
L |
anchura del rodamiento [mm] |
|
L f |
anchura de rodamiento activa [mm] |
|
p 0 |
presión de entrada de lubricante [MPa] |
|
T U |
temperatura del área circundante más próxima al rodamiento [°C]. |
|
T V |
temperatura media del lubricante en la salida del rodamiento [°C]. |
|
T 0 |
temperatura de entrada del lubricante [°C] |
|
v H |
velocidad circunferencial del cojinete transversal del rodamiento [m s -1 ]. |
|
v V |
velocidad del caudal de aire [m s -1 ]. |
|
α W |
factor de eliminación de calor [W m -2 K -1 ]. |
| ε |
excentricidad relativa de cojinete transversal [-] |
| η |
viscosidad dinámica del lubricante a su temperatura media en la salida del rodamiento [Pa s] |
|
ρ 20 |
densidad del lubricante a una temperatura de 20 °C [Kg m -3 ]. |
| χ |
factor de refrigeración interna [-] |
| φ |
juego diametral relativo [mm] |
| ω |
velocidad angular efectiva por hidrodinámica del cojinete transversal del rodamiento [s -1 ] |