Seleccione uno de los siguientes tipos de geometría y parámetros de losa:

|
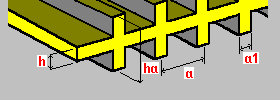
Nervios en una dirección de un lado: h: espesor de la pletina ha: altura del nervio a: separación entre nervios a1: anchura del nervio |
|
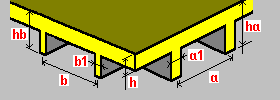
Nervios en una dirección de ambos lados: h: espesor de la pletina ha: altura del nervio a: separación entre nervios a1: anchura del nervio |
|
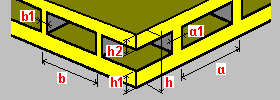
Nervios en dos direcciones de un lado: h: espesor de la pletina ha: altura del nervio hb: altura del nervio a: separación entre nervios a1: anchura del nervio b: separación de los nervios b1: anchura del nervio |
|
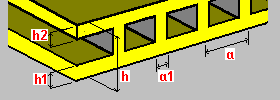
Forjado reticular en una dirección: h: espesor del suelo h1: espesor de la pletina inferior h2: espesor de la pletina superior a: separación de los nervios a1: anchura del nervio |
|
Forjado reticular en dos direcciones: h: espesor del suelo h1: espesor de la pletina inferior h2: espesor de la pletina superior a: separación de los nervios a1: anchura del nervio b: separación de los nervios b1: anchura del nervio |
|
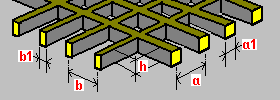
Emparrillado: h: altura del nervio a: separación entre nervios a1: anchura del nervio b: separación de los nervios b1: anchura del nervio |
|
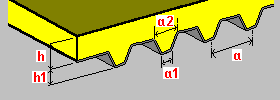
Losa sobre pletina trapezoidal: h: espesor de la pletina h1: altura de la pletina de acero a: separación entre nervios de la pletina de acero a1: anchura del nervio inferior a2: anchura del nervio superior |

|
Ortotropía del material: h: espesor de la pletina n1: coeficiente de rigidez n2: coeficiente de rigidez |
|
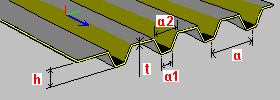
Pletina trapezoidal: h: altura de la pletina t: espesor de la pletina a, a1, a2: dimensiones de un único segmento de la pletina (separación, valores de anchura) |
|
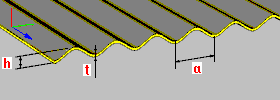
Pletina ondulada: h: altura de la pletina t: espesor de la pletina a: dimensión de un único segmento de pletina (separación) |
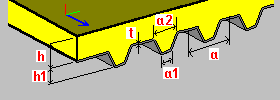
|
Losa unida con pletina trapezoidal: h: espesor de la losa h1: altura de la pletina t: espesor de la pletina a, a1, a2: dimensiones de un único segmento de la pletina (separación, anchura) Es: módulo de Young (acero trapezoidal) vs: coeficiente de Poisson (acero trapezoidal) Eb: módulo de Young (hormigón; valor adoptado basado en un material seleccionado) vb: coeficiente de Poisson (hormigón; valor adoptado basado en un material seleccionado) |
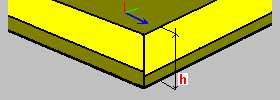
|
Espesor uniforme con rigidez reducida: h: espesor de la losa Coeficientes de reducción de los elementos de la matriz: rigidez de membrana D, rigidez de flexión K y rigidez de corte H. Además, es posible definir un coeficiente de reducción de peso que se tenga en cuenta durante la generación de una carga de peso propio. Los valores de estos coeficientes se definen en el cuadro de diálogo Coeficiente de reducción de rigidez, peso, masa que se abre después de hacer clic en Coeficientes. |
|
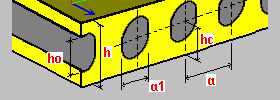
Losa hueca (con huecos circulares u ovalados): h: espesor de la losa a: separación entre rigidizadores, separación entre huecos a1: anchura del hueco/diámetro del círculo ho: altura del hueco (losa con huecos ovalados) hc: distancia entre el centro del hueco y el borde de la losa h1: altura del ala inferior de la losa h2: altura del ala superior de la losa (h2 = h - hc - c/2 - a1/2) c = ho - a1 (losa con huecos ovalados) La opción Descuidar la rigidez de flexión transversal permite omitir o considerar la rigidez de flexión K_YYYY en los cálculos. El hecho de ignorar la rigidez de flexión (dirección Y) tiene como objetivo mejorar el modelado de las losas huecas prefabricadas. |
La ortotropía del material aporta una rigidez diversificada a la pletina que se genera a partir de diferentes propiedades físicas en las direcciones perpendiculares. La diferencia de rigidez se determina mediante los módulos de Young E1 y E2 modificados, respectivamente, en la dirección de ortotropía seleccionada x, y. Los módulos E1 y E2 son el resultado del material seleccionado y los coeficientes n1 y n2 definidos por el usuario. Para ambas direcciones, se adopta un coeficiente de Poisson constante. Este tipo de ortotropía se puede utilizar para crear un modelo de losas de hormigón armado con armadura bidireccional.
El coeficiente de rigidez de las losas de hormigón armado con armadura bidireccional se puede definir con la siguiente fórmula. Suponiendo que el material de la losa sea linealmente elástico, el coeficiente de rigidez de la dirección paralela a la dirección de la armadura es igual a:
n = 1+ 12/(h*h) * e*e * m * u / (1+ m*u)
donde:
h es la altura de una sección de losa.
m = Ez/Eb es la relación entre el módulo de acero y el módulo de hormigón de Young.
e es la distancia entre el centro de gravedad de la armadura y el plano medio de una losa.
u es la densidad del armado, expresado como fracción decimal (un área de sección de las barras de armadura referida al área de unidad de una sección de losa).
Consulte también: