Las fuerzas estáticas aplicadas a una estructura influyen en la frecuencia de las vibraciones de la estructura. El análisis modal comúnmente utilizado (que determina las vibraciones de una estructura) no reconoce la influencia de las fuerzas estáticas. Para aproximarse a las condiciones reales en las que funciona una estructura, los cálculos realizados en Robot pueden llevarse a cabo según el análisis modal reconociendo las fuerzas estáticas aplicadas en dicho análisis.
Existen dos fases de cálculos de vibración de la estructura que reconocen el funcionamiento de las fuerzas estáticas. Estos análisis presentan una correlación estática entre la tensión y la deformación bajo la influencia de una carga estática definida.
Etapa 1: Lineal
donde:
xst: vector desconocido del estado estático
b: vector de una carga estática definida (vector de carga estática)
K: matriz de rigidez
L (xst, b): operador no lineal.
El vector de carga estática b puede ser un caso de carga simple o una combinación de casos de carga definidos.
Etapa 2: Análisis modal (no lineal)
, ( 2a )
donde:
Ks : matriz de rigidez de tensión, originada a partir de las tensiones en el estado estático
M: matriz de masas
ωi2: valor propio(ωi = pulsación)
Φ: vector propio.
Para resolver un problema estático no lineal (modal), se utilizan los mismos métodos que en el análisis estático no lineal. En el caso de un problema estático lineal, se cumple la siguiente correlación 
, donde G es una matriz de rigidez geométrica.
Los valores positivos de ωi (ωi > 0) describen estados estables de equilibrio, mientras que los valores negativos (ωi < 0) se corresponden a estados de equilibrio inestables. A su vez, el valor cero (ωi = 0) indica la falta de estabilidad (pandeo).
Si la matriz K + Ks (xst) deja de determinarse positivamente, la carga estática se aproxima al valor crítico (pandeo). Durante el análisis del problema estático no lineal (modal), no se consigue la convergencia. Si se selecciona el enfoque lineal (una etapa del análisis estático) y la matriz no se determina positivamente, se recomienda detener el cálculo, ya que los cálculos posteriores no tienen ningún sentido.
Ejemplo
Observe el ejemplo de la estructura que se muestra en el siguiente dibujo. N hace referencia a una carga estática.
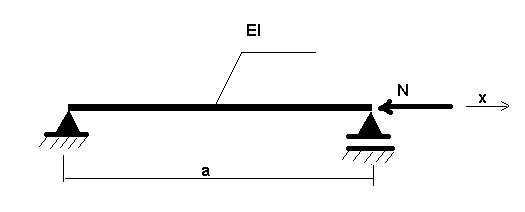
La siguiente fórmula describe su comportamiento.
, ( 3 )
donde:
w: desplazamientos debidos a la flexión
ρ: espesor de material
F: superficie de la sección.
La solución a esta fórmula se buscará mediante la fórmula siguiente:
( 4 )
Una vez que se introduce la expresión ( 4 ) en la fórmula ( 3 ), se obtiene lo siguiente.
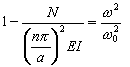, ( 5 )
donde:
: carga crítica
ω02: valor propio para N=0 (resultado del análisis modal normal).
Después de transformar la fórmula final, se obtiene lo siguiente.
, ( 6 )
donde ω2 : valor propio obtenido para la estructura sometida a la operación de la carga estática N.
El resultado de las consideraciones anteriores se presenta gráficamente en el dibujo siguiente.
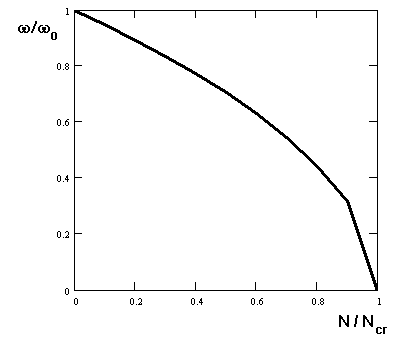
En conclusión, para las estructuras reales la correlación ω= ω(b) suele ser ligeramente más compleja que la obtenida a partir de la fórmula (6).