El método de iteración en el subespacio por bloques se utiliza para resolver el problema con valores propios generalizado.
Los problemas con valores propios generalizados se abordan durante el análisis modal o de pandeo de una estructura.
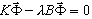
Problema con valores propios generalizado (1)
- K representa la matriz de rigidez.
- B = M: matriz de masas en el caso del análisis dinámico; en los casos restantes B = Ks, donde Ks es la matriz de rigidez de tensión originada en la linealización del operador no lineal adecuado en el caso del análisis de pandeo.
- λ representa el valor propio.
- Φ representa el vector propio.
El método de iteración en el subespacio por bloques es el más adecuado cuando se obtiene un número considerable de pares propios (valores propios y vectores propios) para una estructura. Normalmente, el número es considerable cuando es superior a diez.
El método de iteración en el subespacio por bloques funciona con todos los tipos de matrices de masa, es decir, coherentes, concentradas con rotaciones o concentradas sin rotaciones. El rango de aplicación se limita al análisis modal. Si se selecciona Lanczos, se activan los dos modos restantes: pseudomodal y sísmico.
La opción Verificación de Sturm determina los valores propios omitidos durante el proceso de verificación.
El método de iteración en el subespacio por bloques consiste en iteraciones simultáneas de un vector en el subespacio con una dimensión determinada. Cada vector para el que se ha realizado el proceso de convergencia se elimina del subespacio de trabajo y se añade un nuevo vector inicial en su lugar. La ortogonalidad de los vectores se garantiza en cada paso iterativo. Se aplica el siguiente criterio de convergencia:
![]() ( 2 )
( 2 )
donde:
i, k: el número de modo y el número de pasos de iteración respectivamente.
tol: tolerancia definida en el campo de edición "Tolerancia".
Los resultados de los análisis modales y de pandeo se determinan con cierta precisión mediante la siguiente fórmula:
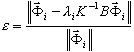 ( 3 )
( 3 )
Si el proceso de convergencia es lento, se recomienda aplicar el procedimiento de desplazamientos en el análisis modal:
![]() ( 4 )
( 4 )
donde:
Kσ = K - σ M,
σ: valor de desplazamiento.
El número de iteraciones entre dos desplazamientos sucesivos se considera el parámetro de este procedimiento.
El procedimiento de desplazamiento no debe aplicarse al análisis de los problemas de pandeo, ya que existe el riesgo de desplazar los espectros de los valores propios en la dirección de la carga crítica negativa (posiblemente sin tener en cuenta las cargas críticas positivas) cuando la estructura tiene valores propios negativos.
Los pares propios determinados se ordenan de la siguiente manera: | λ1 | ≤ | λ 2 | ≤ ... ≤ | λ n |, lo que provoca que los parámetros mínimos de la carga crítica se ubiquen en la parte superior de la tabla con los resultados.
Consulte también:
Iteración en el subespacio por bloques: aplicación de desplazamiento